Article contents
Characterisation Results for Steiner Triple Systems and Their Application to Edge-Colourings of Cubic Graphs
Published online by Cambridge University Press: 20 November 2018
Abstract
It is known that a Steiner triple system is projective if and only if it does not contain the four-triple configuration 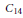 ${{C}_{14}}$. We find three configurations such that a Steiner triple system is affine if and only if it does not contain one of these configurations. Similarly, we characterise Hall triple systems using two forbidden configurations.
${{C}_{14}}$. We find three configurations such that a Steiner triple system is affine if and only if it does not contain one of these configurations. Similarly, we characterise Hall triple systems using two forbidden configurations.
Our characterisations have several interesting corollaries in the area of edge-colourings of graphs. A cubic graph  $G$ is
$G$ is  $S$-edge-colourable for a Steiner triple system
$S$-edge-colourable for a Steiner triple system  $S$ if its edges can be coloured with points of
$S$ if its edges can be coloured with points of  $S$ in such a way that the points assigned to three edges sharing a vertex form a triple in
$S$ in such a way that the points assigned to three edges sharing a vertex form a triple in  $S$. Among others, we show that all cubic graphs are
$S$. Among others, we show that all cubic graphs are  $S$-edge-colourable for every non-projective non-affine point-transitive Steiner triple system
$S$-edge-colourable for every non-projective non-affine point-transitive Steiner triple system  $S$.
$S$.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2010
References
- 7
- Cited by


