Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T07:11:00.770Z Has data issue: false hasContentIssue false
  • English
  • Français

Central Sequence Algebras of a Purely Infinite Simple C*-algebra

Published online by Cambridge University Press:  20 November 2018

Akitaka Kishimoto
Akitaka Kishimoto*
Affiliation:
Department of Mathematics, Hokkaido University, Sapporo 060-0810, Japan e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We are concerned with a unital separable nuclear purely infinite simple 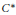${{C}^{*}}$-algebra $A$ satisfying UCT with a Rohlin flow, as a continuation of [12]. Our first result (which is independent of the Rohlin flow) is to characterize when two central projections in $A$ are equivalent by a central partial isometry. Our second result shows that the $\text{K}$-theory of the central sequence algebra 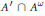${A}'\cap {{A}^{\omega }}$ (for an 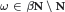$\omega \in \beta \text{N }\!\!\backslash\!\!\text{ N}$) and its fixed point algebra under the flow are the same (incorporating the previous result). We will also complete and supplement the characterization result of the Rohlin property for flows stated in [12].

Keywords

46L40
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 56 , Issue 6 , 01 December 2004 , pp. 1237 - 1258
Copyright
Copyright © Canadian Mathematical Society 2004

References

[1] Bratteli, O., Elliott, G.A., Evans, D.E. and Kishimoto, A., Homotopy of a pair of approximately commuting unitaries in a simple C*-algebra. J. Funct. Anal. 160(1998), 466–523.Google Scholar
[2] Bratteli, O., On the classification of C*-algebras of real rank zero. III. The infinite case Fields Inst. Commun. 20(1998), 11–72.Google Scholar
[3] Bratteli, O. and Kishimoto, A., Trace scaling automorphisms of certain stable AF algebras, II, Q. J. Math. 51(2000), 131–154.Google Scholar
[4] Bratteli, O. and Robinson, D.W., Operator algebras and quantum statistical mechanics, I. Springer-Verlag, New York, 1979.Google Scholar
[5] Elliott, G.A., Normal elements of a simple C*-algebra. In: Algebraic methods in operator theory, Curto, R.E. and Jorgensen, P. E.T. eds., Birkhauser, Boston, 1994, pp. 109–123.Google Scholar
[6] Evans, D.E. and Kishimoto, A., Trace scaling automorphisms of certain stable AF algebras. Hokkaido Math. J. 26(1997), 211–224.Google Scholar
[7] Exel, R. and Loring, T.A., Invariants of almost commuting unitaries. J. Funct. Anal. 95(1991), 364–376.Google Scholar
[8] Kirchberg, E. and Phillips, N.C., Embedding of exact C*-algebras in the Cuntz algebra O2. J. Reine Angew. Math. 525(2000), 17–53.Google Scholar
[9] Kirchberg, E., Embedding of continuous fields of C*-algebras in the Cuntz algebra O2. J. Reine Angew. Math. 525(2000), 55–94.Google Scholar
[10] Kishimoto, A., A Rohlin property for one-parameter automorphism groups. Comm. Math. Phys. 179(1996), 599–622.Google Scholar
[11] Kishimoto, A., Rohlin flows on the Cuntz algebra O2. Internat. J. Math. 13(2002), 1065–1094.Google Scholar
[12] Kishimoto, A., Rohlin property for flows. In: Advances in Quantum Dynamics, Price, G.L. et al. eds., Contemporary Math. 335, 2003, pp. 195–207.Google Scholar
[13] Loring, T.A., K-theory and asymptotically commuting matrices. Canad. J. Math. 40(1988), 197–216.Google Scholar
[14] Nakamura, H., Aperiodic automorphisms of nuclear purely infinite simple C*-algebras, Ergodic Theory Dynam. Sys. 20(2000), 1749–1765.Google Scholar
[15] Rørdam, M., Classification of certain infinite simple C*-algebras, III. Fields Inst. Commun. 13(1997), 257–282.Google Scholar
[16] Sakai, S., Operator algebras in dynamical systems. Cambridge Univ. Press, Cambridge, 1991.Google Scholar
[17] Zhang, S., A property of purely infinite simple C*-algebras. Proc. Amer.Math. Soc. 109(1990), 717–720.Google Scholar