The Central Limit Theorem for Subsequences in Probabilistic Number Theory

Abstract

Let 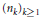${{\left( {{n}_{k}} \right)}_{k\ge 1}}$ be an increasing sequence of positive integers, and let 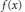$f\left( x \right)$ be a real function satisfying

1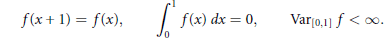

$$f\left( x+1 \right)=f\left( x \right),\int\limits_{0}^{1}{f\left( x \right)}dx=0,\text{Va}{{\text{r}}_{\left[ 0,1 \right]}}f<\infty $$

If 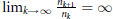${{\lim }_{k\to \infty }}\frac{{{n}_{k+1}}}{{{n}_{k}}}=\infty $ the distribution of

2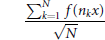

$$\frac{\sum\nolimits_{k=1}^{N}{f\left( {{n}_{k}}x \right)}}{\sqrt{N}}$$

converges to a Gaussian distribution. In the case

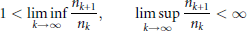$$1<\underset{k\to \infty }{\mathop{\lim \inf }}\,\,\frac{{{n}_{k+1}}}{{{n}_{k}}},\,\,\underset{k\to \infty }{\mathop{\text{lim}\,\text{sup}}}\,\,\frac{{{n}_{k+1}}}{{{n}_{k}}}<\infty$$

there is a complex interplay between the analytic properties of the function 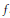$f$, the number-theoretic properties of 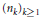${{\left( {{n}_{k}} \right)}_{k\ge 1}}$, and the limit distribution of (2).

In this paper we prove that any sequence 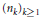${{\left( {{n}_{k}} \right)}_{k\ge 1}}$ satisfying 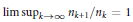$\lim {{\sup }_{k\to \infty }}{{n}_{k+1}}/{{n}_{k}}=1$ contains a nontrivial subsequence 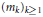${{\left( {{m}_{k}} \right)}_{k\ge 1}}$ such that for any function satisfying (1) the distribution of

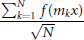$$\frac{\sum\nolimits_{k=1}^{N}{f\left( {{m}_{k}}x \right)}}{\sqrt{N}}$$

converges to a Gaussian distribution. This result is best possible: for any 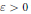$\varepsilon >0$ there exists a sequence 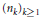${{\left( {{n}_{k}} \right)}_{k\ge 1}}$ satisfying lim 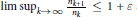$\underset{k\to \infty }{\mathop{\sup }}\,\frac{{{n}_{k+1}}}{{{n}_{k}}}\le 1+\varepsilon$ such that for every nontrivial subsequence 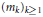${{\left( {{m}_{k}} \right)}_{k\ge 1}}$ of 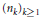${{\left( {{n}_{k}} \right)}_{k\ge 1}}$ the distribution of (2) does not converge to a Gaussian distribution for some 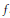$f$.

Our result can be viewed as a Ramsey type result: a sufficiently dense increasing integer sequence contains a subsequence having a certain requested number-theoretic property.