Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T13:02:50.113Z Has data issue: false hasContentIssue false
  • English
  • Français

A Central Limit Theorem and Law of the Iterated Logarithm for a Random Field with Exponential Decay of Correlations

Published online by Cambridge University Press:  20 November 2018

Byron Schmuland  and
Wei Sun
Byron Schmuland
Affiliation:
Department of Mathematical and Statistical Sciences, University of Alberta, Edmonton, Alberta, T6G 2G1 e-mail: [email protected]
Wei Sun
Affiliation:
Department of Mathematical and Statistical Sciences, University of Alberta, Edmonton, Alberta, T6G 2G1 e-mail: [email protected] and Institute of Applied Mathematics, Chinese Academy of Sciences, Beijing 100080, China
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [6], Walter Philipp wrote that “… the law of the iterated logarithm holds for any process for which the Borel-Cantelli Lemma, the central limit theorem with a reasonably good remainder and a certain maximal inequality are valid.” Many authors [1], [2], [4], [5], [9] have followed this plan in proving the law of the iterated logarithm for sequences (or fields) of dependent random variables.

We carry on this tradition by proving the law of the iterated logarithm for a random field whose correlations satisfy an exponential decay condition like the one obtained by Spohn [8] for certain Gibbs measures. These do not fall into the 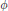$\phi $-mixing or strong mixing cases established in the literature, but are needed for our investigations [7] into diffusions on configuration space.

The proofs are all obtained by patching together standard results from [5], [9] while keeping a careful eye on the correlations.

Keywords

60F9960G60law of the iterated logarithm
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 56 , Issue 1 , 01 February 2004 , pp. 209 - 224
Copyright
Copyright © Canadian Mathematical Society 2004

References

[1] Deo, C. M. and Wong, H. S-F., On Berry-Esseen approximation and a functional LIL for a class of dependent random fields. Pacific J. Math. 91(1980), 269–275.Google Scholar
[2] Iosifescu, M., The law of the iterated logarithm for a class of dependent random variables. Theory Probab. Appl. 13(1968), 304–313.Google Scholar
[3] Kondratiev, Yu. G., Minlos, R. A., Röckner, M. and Shchepan'uk, G. V., Exponential mixing for classical continuous systems. In: Stochastic processes, physics and geometry: new interplays, I (Leipzig, 1999), CMS Conf. Proc. 28, Amer. Math. Soc., 2000, 243–254.Google Scholar
[4] Nahapetian, B., Limit Theorems and Some Applications in Statistical Physics. Teubner Texts in Mathematics 123, B. G. Teubner Verlag, Stuttgart, 1991.Google Scholar
[5] Oodaira, H. and Yoshihara, K., The law of the iterated logarithm for stationary processes satisfying mixing conditions. Kodai Math. Sem. Rep. 23(1971), 311–334.Google Scholar
[6] Philipp, W., The law of the iterated logarithm for mixing stochastic processes. Ann. Math. Statist. 40(1969), 1985–1991.Google Scholar
[7] Schmuland, B. and Sun, W., The law of large numbers and the law of the iterated logarithm for Infinite dimensional interacting diffusion processes. To appear in: Infinite Dimensional Analysis, Quantum Probability, and Related Topics.Google Scholar
[8] Spohn, H., Equilibrium fluctuations for interacting Brownian particles. Commun. Math. Phys. 103(1986), 1–33.Google Scholar
[9] Yoshihara, K., The Borel-Cantelli lemma for strong mixing sequences of events and their applications to LIL. Kodai Math. J. 2(1979), 148–157.Google Scholar