Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T05:27:25.834Z Has data issue: false hasContentIssue false
  • English
  • Français

Central Idempotent Measures on Unitary Groups

Published online by Cambridge University Press:  20 November 2018

Daniel Rider
Daniel Rider*
Affiliation:
University of Wisconsin, Madison, Wisconsin
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a locally compact group and M(G) the space of finite regular Borel measures on G. If μ and v are in M(G), their convolution is defined by

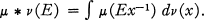
Thus, if f is a continuous bounded function on G,

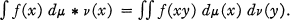
μ is central if μ(Ex) = μ(xE) for all x ∈ G and all measurable sets E. μ is idempotent if μ * μ = μ.

The idempotent measures for abelian groups have been classified by Cohen [1]. In this paper we will show that for a certain class of compact groups, containing the unitary groups, the central idempotents can be characterized. The method consists of showing that, in these cases, the central idempotents arise from idempotents on abelian groups and applying Cohen's result.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 22 , Issue 4 , 01 August 1970 , pp. 719 - 725
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Cohen, P. J., On a conjecture of Littlewood and idempotent measures, Amer. J. Math. 82 (1960), 191–212.Google Scholar
2. Helgason, S., Lacunary Fourier series on noncommutative groups, Proc. Amer. Math. Soc. 9 (1958), 782–790.Google Scholar
3. Ito, T. and Amemiya, I., A simple proof of the theorem of P. J. Cohen, Bull. Amer. Math. Soc. 70 (1964), 774–776.Google Scholar
4. Kelley, J. L., Averaging operators on C°°(Z), Illinois J. Math. 2 (1958), 214–223.Google Scholar
5. Parthasarathy, K. R., A note on idempotent measures in topological groups, J. London Math. Soc. 42 (1967), 534–536.Google Scholar
6. Rudin, W., Fourier analysis on groups (Interscience, New York, 1962).Google Scholar
7. Weyl, H., The classical groups (Princeton Univ. Press, Princeton, N.J., 1946).Google Scholar