Article contents
C*-Convexity and Matricial Ranges
Published online by Cambridge University Press: 20 November 2018
Abstract
C* -convex sets in matrix algebras are convex sets of matrices in which matrix-valued convex coefficients are admitted along with the usual scalar-valued convex coefficients. A Carathéodory-type theorem is developed for C*-convex hulls of compact sets of matrices, and applications of this theorem are given to the theory of matricial ranges. If T is an element in a unital C*-algebra 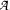 , then for every n ∈ N, the n x n matricial range Wn(T) of T is a compact C* -convex set of n x n matrices. The basic relation W1(T) = conv σ-(T) is well known to hold if T exhibits the normal-like quality of having the spectral radius of β T + μ 1 coincide with the norm ||β T + μ 1|| for every pair of complex numbers β and μ. An extension of this relation to the matrix spaces is given by Theorem 2.6: Wn (T) is the C*-convex hull of the n x n matricial spectrum σn(T) of T if, for every B,M ∈ ℳn, the norm of T ⊗ B + 1 ⊗ M in
, then for every n ∈ N, the n x n matricial range Wn(T) of T is a compact C* -convex set of n x n matrices. The basic relation W1(T) = conv σ-(T) is well known to hold if T exhibits the normal-like quality of having the spectral radius of β T + μ 1 coincide with the norm ||β T + μ 1|| for every pair of complex numbers β and μ. An extension of this relation to the matrix spaces is given by Theorem 2.6: Wn (T) is the C*-convex hull of the n x n matricial spectrum σn(T) of T if, for every B,M ∈ ℳn, the norm of T ⊗ B + 1 ⊗ M in 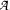 ⊗ ℳn is the maximum value in {||∧⊗B + 1 ⊗M|| : Λ ∈ σn (T)}. The spatial matricial range of a Hilbert space operator is the analogue of the classical numerical range, although it can fail to be convex if n > 1. It is shown in § 3 that if T has a normal dilation N with σ (N) ⊂ σ (T), then the closure of the spatial matricial range of T is convex if and only if it is C*-convex.
⊗ ℳn is the maximum value in {||∧⊗B + 1 ⊗M|| : Λ ∈ σn (T)}. The spatial matricial range of a Hilbert space operator is the analogue of the classical numerical range, although it can fail to be convex if n > 1. It is shown in § 3 that if T has a normal dilation N with σ (N) ⊂ σ (T), then the closure of the spatial matricial range of T is convex if and only if it is C*-convex.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1992
References
- 11
- Cited by


