Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-20T12:38:26.176Z Has data issue: false hasContentIssue false
  • English
  • Français

Categorical Aspects of Quantum Groups: Multipliers and Intrinsic Groups

Published online by Cambridge University Press:  20 November 2018

Matthew Daws
Matthew Daws*
Affiliation:
School of Mathematics, University of Leeds, Leeds LS2 9JT, UK e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that the assignment of the (left) completely bounded multiplier algebra 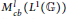$M_{cb}^{l}({{L}^{1}}(\mathbb{G}))$ to a locally compact quantum group 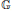$\mathbb{G}$, and the assignment of the intrinsic group, form functors between appropriate categories. Morphisms of locally compact quantum groups can be described by Hopf $*$-homomorphisms between universal 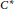${{C}^{*}}$-algebras, by bicharacters, or by special sorts of coactions. We show that the whole theory of completely bounded multipliers can be lifted to the universal 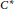${{C}^{*}}$-algebra level, and that the different pictures of both multipliers (reduced, universal, and as centralisers) and morphisms then interact in extremely natural ways. The intrinsic group of a quantum group can be realised as a class of multipliers, and so our techniques immediately apply. We also show how to think of the intrinsic group using the universal 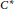${{C}^{*}}$-algebra picture, and then, again, how the differing views on the intrinsic group interact naturally with morphisms. We show that the intrinsic group is the “maximal classical” quantum subgroup of a locally compact quantum group, that it is even closed in the strong Vaes sense, and that the intrinsic group functor is an adjoint to the inclusion functor from locally compact groups to quantum groups.

Keywords

20G4222D2543A2243A3543A9546L5246L8947L25locally compact quantum groupmorphismintrinsic groupmultipliercentraliser
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 68 , Issue 2 , 01 April 2016 , pp. 309 - 333
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Aristov, O. Y., Amenability and compact type for Hopf-von Neumann algebras from the homological point of view. In: Banach algebras and their applications, Contemp. Math., 363, American Mathematical Society, Providence, RI,2004, pp. 15–37.Google Scholar
[2] Baaj, S. and Vaes, S., Double crossed products of locally compact quantum groups. J. Inst. Math. Jussieu 4(2005), 135–173. http://dx.doi.Org/10.1017/S1474748005000034 Google Scholar
[3] Bédos, E. and Tuset, L., Amenability and co-amenability for locally compact quantum groups. Internat. J. Math. 14(2003), no. 8, 865–884.http://dx.doi.Org/10.1142/S0129167X03002046 Google Scholar
[4] Brown, N. and Ozawa, N., C*-algebras and finite-dimensional approximations. Graduate Studies in Mathematics, 88, American Mathematical Society, Providence, RI, 2008.http://dx.doi.Org/10.1090/gsm/088 Google Scholar
[5] De Cannière, J., On the intrinsic group of a Kac algebra. Proc. London Math. Soc. 40(1980), 1–20.http://dx.doi.Org/10.1112/plms/s3-40.1.1 Google Scholar
[6] Dales, H. G., Banach algebras and automatic continuity. London Mathematical Society Monographs, New Series, 24, The Clarendon Press, Oxford University Press, New York, 2000.Google Scholar
[7] Daws, M., Completely positive multipliers of quantum groups. Internat. J. Math. 23(2012), 1250132.http://dx.doi.org/10.1142/S0129167X12501327 Google Scholar
[8] Daws, M., Multipliers of locally compact quantum groups via Hilbert C*-modules. J. Lond. Math. Soc. 84(2011), no. 2, 385–407.http://dx.doi.Org/10.1112/jlms/jdrOI3 Google Scholar
[9] Daws, M. and Le Pham, H., Isometries between quantum convolution algebras. Q. J. Math. 64(2013), no. 2, 373–396.http://dx.doi.Org/10.1093/qmath/has008 Google Scholar
[10] Daws, M., Kasprzak, P., Skalski, A., and Soltan, P., Closed quantum subgroups of locally compact quantum groups. Adv. Math. 231(2012), no. 6, 3473–3501.http://dx.doi.Org/10.1016/j.aim.2012.09.002 Google Scholar
[11] Effros, E. G. and Ruan, Z.-J., Operator spaces. London Mathematical Society Monographs, New Series, 23, The Clarendon Press, Oxford University Press, New York, 2000.Google Scholar
[12] Herz, C., Harmonic synthesis for subgroups. Ann. Inst. Fourier(Grenoble) 23(1973), no. 3, 91–123.http://dx.doi.org/10.5802/aif.473 Google Scholar
[13] Hu, Z., Neufang, M., and Ruan, Z.-J., Completely bounded multipliers over locally compact quantum groups. Proc. Lond. Math. Soc. 103(2011), no. 1,1–39.http://dx.doi.Org/10.1112/plms/pdqO41 Google Scholar
[14] Junge, M., Neufang, M., and Ruan, Z.-J., A representation theorem for locally compact quantum groups. Internat. J. Math. 20(2009), no. 3, 377–400.http://dx.doi.org/10.1142/S0129167X09005285 Google Scholar
[15] Kalantar, M., Representation of left centralizers for actions of locally compact quantum groups. Internat. J. Math. 24(2013), 1350025.http://dx.doi.Org/10.1142/S0129167X13500250 Google Scholar
[16] Kalantar, M. and Neufang, M., From quantum groups to groups. Canad. J. Math. 65(2013), no. 5, 1073–1094.http://dx.doi.org/10.4153/CJM-2012-047-x Google Scholar
[17] Kustermans, J., Locally compact quantum groups in the universal setting. Internat. J. Math. 12(2001), no. 3, 289–338.http://dx.doi.Org/10.1142/S0129167X01000757 Google Scholar
[18] Kustermans, J., Locally compact quantum groups. In Quantum independent increment processes. I, Lecture Notes in Math., 1865, Springer, Berlin, 2005, pp. 99–180.Google Scholar
[19] Kustermans, J. and Vaes, S., Locally compact quantum groups in the von Neumann algebraic setting. Math. Scand. 92(2003), no. 1, 68–92.Google Scholar
[20] Kustermans, J. and Vaes, S., Locally compact quantum groups. Ann. Sci. École Norm. Sup. (4) 33(2000), no. 6, 837–934. Google Scholar
[21] Lance, E. C., Hilbert C*-modules. A toolkit for operator algebraists. Cambridge University Press, Cambridge, 1995.http://dx.doi.Org/10.1017/CBO9780511526206 Google Scholar
[22] Leinster, T., Basic category theory. Cambridge Studies in Advanced Mathematics, 143, Cambridge University Press, Cambridge, 2014.Google Scholar
[23] Masuda, T., Nakagami, Y., and Woronowicz, S. L., A C*-algebraic framework for quantum groups. Internat. J. Math. 14(2003), no. 9, 903–1001.http://dx.doi.Org/10.1142/S0129167X03002071 Google Scholar
[24] Meyer, R., Roy, S., and Woronowicz, S. L., Homomorphisms of quantum groups. Münster J. Math. 5(2012), 1–24.Google Scholar
[25] Ng, C.-K., Morphisms of multiplicative unitaries. J. Operator Theory 38(1997), no. 2, 203–224.Google Scholar
[26] Sołtan, P. and Woronowicz, S. L., From multiplicative unitaries to quantum groups. II. J. Funct. Anal. 252(2007), no. 1, 42–67.http://dx.doi.Org/10.1016/j.jfa.2007.07.006 Google Scholar
[27] Spronk, N., Measurable Schur multipliers and completely bounded multipliers of the Fourier algebras. Proc. London Math. Soc. 89(2004), no. 1,161–192.http://dx.doi.Org/10.1112/S0024611504014650 Google Scholar
[28] Vaes, S., A new approach to induction and imprimitivity results. J. Funct. Anal. 229(2005), no. 2, 317–374.http://dx.doi.Org/10.1016/j.jfa.2004.11.016 Google Scholar
[29] Vaes, S., Locally compact quantum groups. PhD. thesis, Katholieke Universiteit Leuven, 2001.http://wis.kuleuven.be/analyse/stefaan/ Google Scholar
[30] Vaes, S. and van Daele, A., Hopf C*-algebras. Proc. London Math. Soc. 82(2001), no. 2, 337–384.http://dx.doi.Org/10.1112/S002461150101276X Google Scholar
[31] Woronowicz, S. L., From multiplicative unitaries to quantum groups. Internat. J. Math. 7(1996), no. 1,127–149.http://dx.doi.Org/10.1142/S0129167X96000086 Google Scholar