Casselman’s Basis of Iwahori Vectors and the Bruhat Order

Abstract

W. Casselman defined a basis 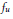${{f}_{u}}$ of Iwahori fixed vectors of a spherical representation 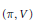$(\pi ,\,V)$ of a split semisimple 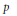$p$-adic group 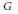$G$ over a nonarchimedean local field $F$ by the condition that it be dual to the intertwining operators, indexed by elements 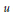$u$ of the Weyl group 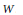$W$. On the other hand, there is a natural basis 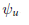${{\psi }_{u}}$, and one seeks to find the transition matrices between the two bases. Thus, let 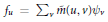${{f}_{u}}\,=\,{{\sum }_{v}}\overset{\tilde{\ }}{\mathop{m}}\,(u,\,v){{\psi }_{v}}$ and ${{\psi }_{u}}\,=\,{{\sum }_{v}}m(u,\,v){{f}_{v}}$. Using the Iwahori–Hecke algebra we prove that if a combinatorial condition is satisfied, then 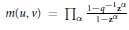$m(u,\,v)\,=\,{{\Pi }_{\alpha }}\,\frac{1-{{q}^{-1}}\,{{z}^{\alpha }}}{1-{{z}^{\alpha }}}$ , where $\mathbf{z}$ are the Langlands parameters for the representation and 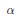$\alpha $ runs through the set 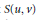$S(u,\,v)$ of positive coroots 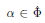$\alpha \,\in \,\hat{\Phi }$ (the dual root systemof 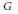$G$) such that 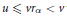$u\,\le \,v{{r}_{\alpha }}\,<\,v$ with 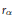${{r}_{\alpha }}$ the reflection corresponding to 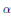$\alpha $. The condition is conjecturally always satisfied if 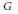$G$ is simply-laced and the Kazhdan–Lusztig polynomial 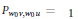${{P}_{{{w}_{0}}v,\,{{w}_{0}}u}}\,=\,1$ with 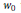${{w}_{0}}$ the long Weyl group element. There is a similar formula for 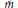$\tilde{m}$ conjecturally satisfied if 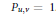${{P}_{u,\,v}}\,=\,1$. This leads to various combinatorial conjectures.