Article contents
Casselman’s Basis of Iwahori Vectors and Kazhdan–Lusztig Polynomials
Published online by Cambridge University Press: 07 January 2019
Abstract
A problem in representation theory of 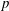 $p$-adic groups is the computation of the Casselman basis of Iwahori fixed vectors in the spherical principal series representations, which are dual to the intertwining integrals. We shall express the transition matrix
$p$-adic groups is the computation of the Casselman basis of Iwahori fixed vectors in the spherical principal series representations, which are dual to the intertwining integrals. We shall express the transition matrix 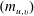 $(m_{u,v})$ of the Casselman basis to another natural basis in terms of certain polynomials that are deformations of the Kazhdan–Lusztig R-polynomials. As an application we will obtain certain new functional equations for these transition matrices under the algebraic involution sending the residue cardinality
$(m_{u,v})$ of the Casselman basis to another natural basis in terms of certain polynomials that are deformations of the Kazhdan–Lusztig R-polynomials. As an application we will obtain certain new functional equations for these transition matrices under the algebraic involution sending the residue cardinality 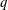 $q$ to
$q$ to 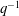 $q^{-1}$. We will also obtain a new proof of a surprising result of Nakasuji and Naruse that relates the matrix
$q^{-1}$. We will also obtain a new proof of a surprising result of Nakasuji and Naruse that relates the matrix 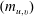 $(m_{u,v})$ to its inverse.
$(m_{u,v})$ to its inverse.
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2018
Footnotes
This work was supported by NSF grant DMS-1601026 and JSPS Grant-in-Aid for Young Scientists (B) 15K17519. We thank the referee for careful reading.
References
- 4
- Cited by


