Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Burbea, Jacob
1981.
Pick's theorem with operator-valued holomorphic functions.
Kodai Mathematical Journal,
Vol. 4,
Issue. 3,
Burbea, Jacob
and
Rao, C.Radhakrishna
1982.
Entropy differential metric, distance and divergence measures in probability spaces: A unified approach.
Journal of Multivariate Analysis,
Vol. 12,
Issue. 4,
p.
575.
Azukawa, Kazuo
and
Burbea, Jacob
1984.
Hessian quartic forms and the Bergman metric.
Kodai Mathematical Journal,
Vol. 7,
Issue. 2,
Azukawa, Kazuo
1985.
Square-integrable holomorphic functions on a circular domain in $C^n$.
Tohoku Mathematical Journal,
Vol. 37,
Issue. 1,
Azukawa, Kazuo
1985.
Curvature operator of the Bergman metric on a homogeneous bounded domain.
Tohoku Mathematical Journal,
Vol. 37,
Issue. 2,
Misra, Gadadhar
and
Sastry, N.S.Narsimha
1990.
Bounded modules, extremal problems, and a curvature inequality.
Journal of Functional Analysis,
Vol. 88,
Issue. 1,
p.
118.
Li, Bo
2011.
The Berezin transform and 𝑚th-order Bergman metric.
Transactions of the American Mathematical Society,
Vol. 363,
Issue. 6,
p.
3031.
Chen, Bo-Yong
Xiong, Yuanpu
and
Zhang, Liyou
2024.
Equality between the Bergman metric and Carathéodory metric.
Proceedings of the American Mathematical Society,


 be a fixed point in
be a fixed point in 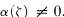 .
.