Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-27T19:04:04.475Z Has data issue: false hasContentIssue false
  • English
  • Français

The C*–algebras of Compact Transformation Groups

Published online by Cambridge University Press:  20 November 2018

Robert J. Archbold  and
Astrid an Huef
Robert J. Archbold
Affiliation:
Institute of Mathematics, University of Aberdeen, Aberdeen AB24 3UE, Scotland, UK e-mail: [email protected]
Astrid an Huef
Affiliation:
Department of Mathematics and Statistics, University of Otago, Dunedin 9054, New Zealand e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We investigate the representation theory of the crossed-product 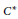${{C}^{*}}$-algebra associated with a compact group 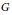$G$ acting on a locally compact space 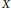$X$ when the stability subgroups vary discontinuously. Our main result applies when 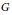$G$ has a principal stability subgroup or 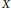$X$ is locally of finite 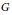$G$-orbit type. Then the upper multiplicity of the representation of the crossed product induced from an irreducible representation 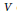$V$ of a stability subgroup is obtained by restricting 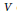$V$ to a certain closed subgroup of the stability subgroup and taking the maximum of the multiplicities of the irreducible summands occurring in the restriction of 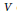$V$. As a corollary we obtain that when the trivial subgroup is a principal stability subgroup; the crossed product is a Fell algebra if and only if every stability subgroup is abelian. A second corollary is that the 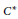${{C}^{*}}$-algebra of the motion group 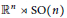${{\mathbb{R}}^{n}}\,\rtimes \,\text{SO}\left( n \right)$ is a Fell algebra. This uses the classical branching theorem for the special orthogonal group 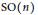$\text{SO}\left( n \right)$ with respect to 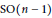$\text{SO}\left( n-1 \right)$. Since proper transformation groups are locally induced from the actions of compact groups, we describe how some of our results can be extended to transformation groups that are locally proper.

Keywords

46L0546L55Compact transformation groupproper actionspectrum of a C*–algebramultiplicity of a representationcrossed–product C*–algebracontinuous–trace C*–algebraFell algebra
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 67 , Issue 3 , 01 June 2015 , pp. 481 - 506
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Abels, H., A universal proper G–space. Math. Z. 159(1978), no. 2,143–158.http://dx.doi.Org/1 0.1007/BF01214487 Google Scholar
[2] Archbold, R. J., Upper and lower multiplicity for irreducible representations ofC––algebras. Proc. London Math. Soc. 69(1994), no. 1,121–143. http://dx.doi.Org/10.1112/plms/s3-69.1.121 Google Scholar
[3] Archbold, R. J., Topologies for primal ideals. J. London Math. Soc. (2) 36(1987), no. 3, 524–542.http://dx.doi.Org/10.1112/jlms/s2-36.3.524 Google Scholar
[4] Archbold, R. J. and Kaniuth, E., Upper and lower multiplicity for irreducible representations of SIN–groups. Illinois J. Math. 43(1999), no. 4, 692–706.Google Scholar
[5] Archbold, R. J. and Kaniuth, E., Stable rank and real rank of compact transformation group C––algebras. Studia Math. 175(2006), no. 2, 103–120. http://dx.doi.org/10.4064/sm175-2-1 Google Scholar
[6] Archbold, R. J. and Somerset, D. W. B., Transition probabilities and trace functions for C––algebras. Math. Scand. 73(1993), no. 1, 81–111.Google Scholar
[7] Archbold, R. J., Somerset, D. W. B., and Spielberg, J. S., Upper multiplicity and bounded trace ideals in C––algebras. J. Funct. Anal. 146(1997), no. 2, 430–463.http://dx.doi.Org/10.1006/jfan.1996.3041 Google Scholar
[8] Archbold, R. J. and Spielberg, J. S., Upper and lower multiplicity for irreducible representations of C––algebras. II. J. Operator Theory 36(1996), no. 2, 201–231.Google Scholar
[9] Baggett, L., A description of the topology on the dual spaces of certain locally compact groups. Trans. Amer. Math. Soc. 132(1968), 175–215. http://dx.doi.org/10.1090/S0002-9947-1968-0409720-2 Google Scholar
[10] Bernât, P., Conze, N., Duflo, M., Lévy–Nahas, M., Raïs, M., Renouard, P., and Vergne, M., Représentations des groupes de Lie résolubles. Monographies de la Société Mathématique de France, 4 Dunod, Paris, 1972.Google Scholar
[11] Bredon, G. E., Introduction to compact transformation groups. Pure and Applied Mathematics, 46, Academic Press, New York–London, 1972.Google Scholar
[12] Deitmar, A. and Echterhoff, S., Principles of harmonie analysis. Universitext, Springer, 2009.Google Scholar
[13] Dixmier, J., C––Algebras. North–Holland Mathematical Library, 15, North–Holland, Amsterdam–New York–Oxford, 1977.Google Scholar
[14] Echterhoff, S., On transformation group C––algebras with continuous trace. Trans. Amer. Math. Soc. 343(1994), no. 1, 117–133.Google Scholar
[15] Echterhoff, S. and Emerson, H., Structure and K–theory of crossed products by proper actions. Expo. Math. 29(2011), no. 3, 300–344. http://dx.doi.Org/10.1016/j.exmath.2011.05.001 Google Scholar
[16] Fell, J. M. G., A Hausdorff topology for the closed subsets of a locally compact non–Hausdorff space. Proc. Amer. Math. Soc. 13(1962), 472–476. http://dx.doi.org/10.1090/S0002-9939-1962-0139135-6 Google Scholar
[17] Fell, J. M. G., Weak containment and induced representations of groups. II. Trans. Amer. Math. Soc. 110(1964), 424–447.Google Scholar
[18] Gootman, E. C. and Lazar, A. J., Applications of non–commutative duality to crossed product C––algebras determined by an action or coaction. Proc. London Math. Soc. 59(1989), no. 3, 593–624.http://dx.doi.org/10.1112/plms/s3-593.593 Google Scholar
[19] Gootman, E. C. and Lazar, A. J., Compact group actions on C– –algebras: an application of non–commutative duality. J. Funct. Anal. 91(1990), no. 2, 237–245. http://dx.doi.org/10.1016/0022-1236(90)90142-8 Google Scholar
[20] Green, P., C– –algebras of transformation groups with smooth orbit space. Pacific J. Math. 72(1977), no. 1, 71–97. http://dx.doi.org/10.2140/pjm.1977.72.71 Google Scholar
[21] Green, P., The local structure of twisted covariance algebras. Acta Math. 140(1978), no. 3-4,191–250 http://dx.doi.org/10.1007/BF02392308 Google Scholar
[22] Hewitt, E. and Ross, K. A., Abstract harmonic analysis. I. Structure of topological groups. Integration theory, group representations. Die Grundlehren der mathematischen Wissenschaften, 115, Academic Press, Inc., Publishers, New York; Springer–Verlag, Berlin–Gôttingen–Heidelberg, 1963.Google Scholar
[23] an Huef, A., The transformation groups whose C– –algebras are Fell algebras. Bull. London Math. Soc. 33(2001), no. 1, 73–76. http://dx.doi.Org/10.1112/blms/33.1.73 Google Scholar
[24] an Huef, A., Integrable actions and the transformation groups whose C*–algebras have bounded trace. Indiana Univ. Math. J. 51(2002), no. 5,1197–1233.http://dx.doi.Org/10.1512/iumj.2OO2.51.2168 Google Scholar
[25] an Huef, A., Kumjian, A., and Sims, A., A Dixmier–Douady theorem for Fell algebras. J. Funct. Anal 260(2011), no. 5, 1543–1581. http://dx.doi.Org/10.1016/j.jfa.2010.11.011 Google Scholar
[26] an Huef, A., Raeburn, I., and Williams, Dana.P, Properties preserved under Morita equivalences of C––algebras. Proc. Amer. Math. Soc. 135(2007), no. 5, 1495–1503.http://dx.doi.org/10.1090/S0002-9939-06-08625-4 Google Scholar
[27] James, G. D., The representation theory of the symmetric groups. Lecture Notes in Mathematics, 682, Springer, Berlin, 1978.Google Scholar
[28] Kaniuth, E., Schlichting, G., and Taylor, K. F., Minimal primal and Glimm ideal spaces of group C––algebras. J. Funct. Anal. 130(1995), no. 1, 43–76.http://dx.doi.Org/10.1006/jfan.1995.1063 Google Scholar
[29] Kaniuth, E. and Taylor, K. F., Induced representations of locally compact groups. Cambridge Tracts in Mathematics, 197, Cambridge University Press, Cambridge, 2013.Google Scholar
[30] Knapp, A. W., Branching theorems for compact symmetric spaces. Represent. Theory 5(2001), 404–436.http://dx.doi.Org/10.1090/S1088-4165-01-00139-X Google Scholar
[31] Marelli, D. and Raeburn, I., Proper actions which are not saturated. Proc. Amer. Math. Soc. 137(2009), no. 7, 2273–2283. http://dx.doi.org/10.1090/S0002-9939-09-09867-0 Google Scholar
[32] Montgomery, D., Orbits of highest dimension. In: Seminar on transformation groups, Ann. of Math., 46, Chapter IX, Princeton Univ. Press, Princeton, NJ, 1960, pp. 117–131.Google Scholar
[33] Murnaghan, F. D., The theory of group representations. Hopkins Press, Baltimore, 1938.Google Scholar
[34] Neumann, K., A description of the Jacobson topology on the spectrum of transformation group C– –algebras by proper actions. PhD thesis, University of Münster, 2011.Google Scholar
[35] Palais, R. S., On the existence of slices for actions of non–compact Lie groups. Ann. of Math. 73(1961), 295–323. http://dx.doi.Org/10.2307/1 970335 Google Scholar
[36] Pedersen, G. K., C– –algebras and their automorphism groups. London Mathematical Society Monographs, 14, Academic Press, London, 1979.Google Scholar
[37] Raeburn, I., Induced C––algebras and a symmetric imprimitivity theorem. Math. Ann. 280(1988), no. 3, 369–387.http://dx.doi.org/10.1007/BF01456331 Google Scholar
[38] Raeburn, I. and Williams, D.P., Morita equivalence and continuous–trace C––algebras. Mathematical Surveys and Monographs, 60, American Mathematical Society, Providence, RI, 1998.Google Scholar
[39] Rieffel, M. A., Proper actions of groups on C––algebras. In: Mappings of operator algebras (Philadelphia, PA, 1988) Progr. Math., 84, Birkhâuser Bsoton, Boston, MA, 1990, pp. 141–182.Google Scholar
[40] Rieffel, M. A., Integrable and proper actions on C– –algebras, and square–integrable representations of groups. Expo. Math. 22(2004), no. 1, 1–53.http://dx.doi.Org/10.101 6/S0723-0869(04)80002-1 Google Scholar
[41] Rosenberg, J., Appendix to “Crossed products of UHF algebras byproduct type actions” [Duke Math. J. 46(1979), no. 1,1–23] by O. Bratteli., Duke Math. J. 46(1979), 25–26.http://dx.doi.org/10.1215/S0012-7094-79-04602-7 Google Scholar
[42] Williams, D. P., The topology on the primitive ideal space of transformation group C––algebras and CCR transformation group C––algebras. Trans. Amer. Math. Soc. 226(1981), no. 2, 335–359.Google Scholar
[43] Williams, D. P., Crossed products of C––algebras. Mathematical Surveys and Monographs, 134, American Mathematical Society, 2007.Google Scholar