Article contents
Bump Functions with Hölder Derivatives
Published online by Cambridge University Press: 20 November 2018
Abstract
We study the range of the gradients of a
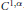 ${{C}^{1,\alpha }}$
-smooth bump function defined on a Banach space. We find that this set must satisfy two geometrical conditions: It can not be too flat and it satisfies a strong compactness condition with respect to an appropriate distance. These notions are defined precisely below. With these results we illustrate the differences with the case of
${{C}^{1,\alpha }}$
-smooth bump function defined on a Banach space. We find that this set must satisfy two geometrical conditions: It can not be too flat and it satisfies a strong compactness condition with respect to an appropriate distance. These notions are defined precisely below. With these results we illustrate the differences with the case of 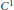 ${{C}^{1}}$-smooth bump functions. Finally, we give a sufficient condition on a subset of
${{C}^{1}}$-smooth bump functions. Finally, we give a sufficient condition on a subset of 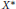 ${{X}^{*}}$ so that it is the set of the gradients of a
${{X}^{*}}$ so that it is the set of the gradients of a 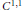 ${{C}^{1,1}}$-smooth bump function. In particular, if
${{C}^{1,1}}$-smooth bump function. In particular, if 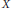 $X$ is an infinite dimensional Banach space with a
$X$ is an infinite dimensional Banach space with a 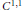 ${{C}^{1,1}}$-smooth bump function, then any convex open bounded subset of
${{C}^{1,1}}$-smooth bump function, then any convex open bounded subset of 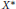 ${{X}^{*}}$ containing 0 is the set of the gradients of a
${{X}^{*}}$ containing 0 is the set of the gradients of a 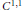 ${{C}^{1,1}}$-smooth bump function.
${{C}^{1,1}}$-smooth bump function.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2004
References
- 1
- Cited by


