A Bott–Borel–Weil Theorem for Diagonal Ind-groups

Abstract

A diagonal ind-group is a direct limit of classical affine algebraic groups of growing rank under a class of inclusions that contains the inclusion

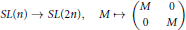$$SL(n)\,\to \,SL(2n),\,\,M\mapsto \,\left( \begin{matrix} M & 0 \\ 0 & M \\ \end{matrix} \right)$$

as a typical special case. If 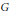$G$ is a diagonal ind-group and 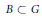$B\,\subset \,G$ is a Borel ind-subgroup, we consider the ind-variety 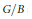$G/B$ and compute the cohomology 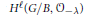${{H}^{\ell }}(G/B,\,{{\mathcal{O}}_{-\lambda }})$ of any 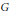$G$-equivariant line bundle 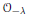${{\mathcal{O}}_{-\lambda }}$ on 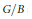$G/B$. It has been known that, for a generic 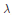$\lambda $, all cohomology groups of 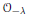${{\mathcal{O}}_{-\lambda }}$ vanish, and that a non-generic equivariant line bundle 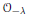${{\mathcal{O}}_{-\lambda }}$ has at most one nonzero cohomology group. The new result of this paper is a precise description of when 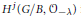${{H}^{j}}(G/B,\,{{\mathcal{O}}_{-\lambda }})$ is nonzero and the proof of the fact that, whenever nonzero, 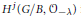${{H}^{j}}(G/B,\,{{\mathcal{O}}_{-\lambda }})$ is a $G$-module dual to a highest weight module. The main difficulty is in defining an appropriate analog 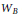${{W}_{B}}$ of the Weyl group, so that the action of 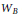${{W}_{B}}$ on weights of 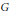$G$ is compatible with the analog of the Demazure “action” of the Weyl group on the cohomology of line bundles. The highest weight corresponding to 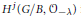${{H}^{j}}(G/B,\,{{\mathcal{O}}_{-\lambda }})$ is then computed by a procedure similar to that in the classical Bott–Borel–Weil theorem.