Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-30T03:59:21.392Z Has data issue: false hasContentIssue false
  • English
  • Français

A Boltzmann Approach to Percolation on Random Triangulations

Part of: Special processes Geometric probability and stochastic geometry Combinatorics

Published online by Cambridge University Press:  07 January 2019

Olivier Bernardi ,
Nicolas Curien  and
Grégory Miermont
Olivier Bernardi
Affiliation:
Department of Mathematics, Brandeis University, USA Email: [email protected]
Nicolas Curien
Affiliation:
Département de Mathématiques de l’Université Paris-Sud, and Institut Universitaire de France Email: [email protected]
Grégory Miermont
Affiliation:
Unité de Mathématiques Pures et Appliquées de l’École Normale Supérieure de Lyon, and Institut Universitaire de France Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the percolation model on Boltzmann triangulations using a generating function approach. More precisely, we consider a Boltzmann model on the set of finite planar triangulations, together with a percolation configuration (either site-percolation or bond-percolation) on this triangulation. By enumerating triangulations with boundaries according to both the boundary length and the number of vertices/edges on the boundary, we are able to identify a phase transition for the geometry of the origin cluster. For instance, we show that the probability that a percolation interface has length $n$ decays exponentially with $n$ except at a particular value 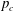$p_{c}$ of the percolation parameter 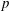$p$ for which the decay is polynomial (of order 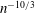$n^{-10/3}$). Moreover, the probability that the origin cluster has size $n$ decays exponentially if 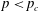$p<p_{c}$ and polynomially if 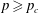$p\geqslant p_{c}$.

The critical percolation value is 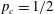$p_{c}=1/2$ for site percolation, and 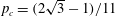$p_{c}=(2\sqrt{3}-1)/11$ for bond percolation. These values coincide with critical percolation thresholds for infinite triangulations identified by Angel for site-percolation, and by Angel and Curien for bond-percolation, and we give an independent derivation of these percolation thresholds.

Lastly, we revisit the criticality conditions for random Boltzmann maps, and argue that at 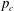$p_{c}$, the percolation clusters conditioned to have size $n$ should converge toward the stable map of parameter 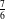$\frac{7}{6}$ introduced by Le Gall and Miermont. This enables us to derive heuristically some new critical exponents.

Keywords

random mapstable mapcritical percolationgasket

MSC classification

Primary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Secondary: 60D05: Geometric probability and stochastic geometry 05A16: Asymptotic enumeration
Type
Article
Information
Canadian Journal of Mathematics , Volume 71 , Issue 1 , February 2019 , pp. 1 - 43
Copyright
© Canadian Mathematical Society 2018 

Footnotes

We thank the Newton institute for hospitality during the Random Geometry program in 2015 where part of this work was completed. We acknowledge the support of the NSF grant DMS-1400859, and of the Agence Nationale de la Recherche via the grants ANR Liouville (ANR-15-CE40-0013) and ANR GRAAL (ANR-14-CE25-0014).

References

Angel, O., Growth and percolation on the uniform infinite planar triangulation . Geom. Funct. Anal. 13(2003), no. 5, 935–974. https://doi.org/10.1007/s00039-003-0436-5.Google Scholar
Angel, O. and Curien, N., Percolations on infinite random maps, half-plane models . Ann. Inst. H. Poincaré Probab. Stat. 51(2015), no. 2, 405–431. https://doi.org/10.1214/13-AIHP583.Google Scholar
Angel, O. and Schramm, O., Uniform infinite planar triangulation . Comm. Math. Phys. 241(2003), no. 2–3, 191–213. https://doi.org/10.1007/s00220-003-0932-3.Google Scholar
Bertoin, J., Curien, N., and Kortchemski, I., Random planar maps and growth-fragmentations . Ann. of Probab. 46(2018), no. 1, 207–260. https://doi.org/10.1214/17-AOP1183.Google Scholar
Borot, G., Bouttier, J., and Guitter, E., Loop models on random maps via nested loops: case of domain symmetry breaking and application to the potts model . J. Phys. A 45(2012), no. 49, 494017. https://doi.org/10.1088/1751-8113/45/49/494017.Google Scholar
Borot, G., Bouttier, J., and Guitter, E., A recursive approach to the O (N) model on random maps via nested loops . J. Phys. A 45(2012), no. 4, 045002. https://doi.org/10.1088/1751-8113/45/4/045002.Google Scholar
Bousquet-Mélou, M. and Jehanne, A., Polynomial equations with one catalytic variable, algebraic series and map enumeration . J. Combin. Theory Ser. B 96(2006), no. 5, 623–672. https://doi.org/10.1016/j.jctb.2005.12.003.Google Scholar
Bouttier, J., Di Francesco, P., and Guitter, E., Planar maps as labeled mobiles . Electron. J. Combin. 11(2004), no. 1, Research Paper 69.Google Scholar
Budd, T., The peeling process of infinite Boltzmann planar maps . Electron. J. Combin. 23(2016), no. 1, Paper 1.28.Google Scholar
Curien, N., Peeling random planar maps. https://www.math.u-psud.fr/∼curien/.Google Scholar
Curien, N. and Kortchemski, I., Percolation on random triangulations and stable looptrees . Probab. Theory Related Fields 163(2015), no. 1–2, 303–337. https://doi.org/10.1007/s00440-014-0593-5.Google Scholar
Curien, N. and Le Gall, J.-F., Scaling limits for the peeling process on random maps . Ann. Inst. Henri Poincaré Probab. Stat. 53(2017), no. 1, 322–357. https://doi.org/10.1214/15-AIHP718.Google Scholar
Curien, N., Le Gall, J.-F., and Miermont, G., The Brownian cactus I. Scaling limits of discrete cactuses . Ann. Inst. Henri Poincaré Probab. Stat. 49(2013), no. 2, 340–373. https://doi.org/10.1214/11-AIHP460.Google Scholar
Flajolet, P. and Sedgewick, R., Analytic combinatorics. Cambridge University Press, Cambridge, 2009. https://doi.org/10.1017/CBO9780511801655.Google Scholar
Gorny, M., Maurel-Segala, E., and Singh, A., The geometry of a critical percolation cluster on the UIPT. 2017. arxiv:1701.01667.Google Scholar
Goulden, I. and Jackson, D., Combinatorial enumeration . Wiley-Interscience Series in Discrete Mathematics. John Wiley and Sons, New York, 1983.Google Scholar
Le Gall, J.-F. and Miermont, G., Scaling limits of random planar maps with large faces . Ann. Probab. 39(2011), no. 1, 1–69. https://doi.org/10.1214/10-AOP549.Google Scholar
Marckert, J.-F. and Miermont, G., Invariance principles for random bipartite planar maps . Ann. Probab. 35(2007), no. 5, 1642–1705. https://doi.org/10.1214/009117906000000908.Google Scholar
Ménard, L., Volumes in the uniform infinite planar triangulation: from skeletons to generating functions. 2016. arxiv:1604.00908.Google Scholar
Ménard, L. and Nolin, P., Percolation on uniform infinite planar maps . Electron. J. Probab. 19(2014), no. 79. https://doi.org/10.1214/EJP.v19-2675.Google Scholar
Miermont, G., An invariance principle for random planar maps. In: Fourth Colloquium on Mathematics and Computer Science Algorithms, Trees, Combinatorics and Probabilities, Discrete Math. Theor. Comput. Sci. Proc., AG, Assoc. Discrete Math. Theor. Comput. Sci., Nancy, 2006, pp. 39–57.Google Scholar
Miermont, G., Invariance principles for spatial multitype Galton–Watson trees . Ann. Inst. Henri Poincaré Probab. Stat. 44(2008), no. 6, 1128–1161. https://doi.org/10.1214/07-AIHP157.Google Scholar
Maple worksheet: site-percolation-triangulations.mws; see https://doi.org/10.4153/CJM-2018-009-x.Google Scholar
Maple worksheet: bond-percolation-triangulations.mws; see https://doi.org/10.4153/CJM-2018-009-x.Google Scholar
Richier, L., Universal aspects of critical percolation on random half-planar maps . Electron. J. Probab. 20(2015), Paper No. 129. https://doi.org/10.1214/EJP.v20-4041.Google Scholar
Richier, L., Limits of the boundary of random planar maps. 2017. arxiv:1704.01950.Google Scholar
Stephenson, R., Local convergence of large critical multi-type Galton–Watson trees and applications to random maps . J. Theoret. Probab. 31(2018), no. 1, 159–205. https://doi.org/10.1007/s10959-016-0707-3.Google Scholar
Tutte, W., A census of slicings . Canad. J. Math. 14(1962), 708–722. https://doi.org/10.4153/CJM-1962-061-1.Google Scholar
Supplementary material: File

Bernardi et al. supplementary material

Bernardi et al. supplementary material 1

Download Bernardi et al. supplementary material(File)
File 428.9 KB
Supplementary material: File

Bernardi et al. supplementary material

Bernardi et al. supplementary material 2

Download Bernardi et al. supplementary material(File)
File 576.2 KB