Hostname: page-component-6bf8c574d5-956mj Total loading time: 0 Render date: 2025-02-24T01:06:23.260Z Has data issue: false hasContentIssue false
  • English
  • Français

BMO Functions and Carleson Measures with Values in Uniformly Convex Spaces

Published online by Cambridge University Press:  20 November 2018

Caiheng Ouyang  and
Quanhua Xu
Caiheng Ouyang
Affiliation:
Wuhan Institute of Physics and Mathematics, Chinese Academy of Sciences, Wuhan, China, e-mail: [email protected]
Quanhua Xu
Affiliation:
Laboratoire de Mathématiques, Université de Franche-Comté, Besanҫon, France, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper studies the relationship between vector-valued $\text{BMO}$ functions and the Carleson measures defined by their gradients. Let 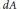$dA$ and 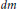$dm$ denote Lebesgue measures on the unit disc 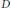$D$ and the unit circle 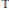$\mathbb{T}$, respectively. For 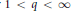$1\,<\,q\,<\,\infty $ and a Banach space $B$, we prove that there exists a positive constant $c$ such that

$$\underset{{{z}_{0}}\in D}{\mathop{\sup }}\,{{\int }_{D}}{{\left( 1-\left| z \right| \right)}^{q-1}}{{\left\| \nabla f\left( z \right) \right\|}^{q}}{{P}_{{{Z}_{0}}}}\left( z \right)dA\left( z \right)\le {{c}^{q}}\underset{{{z}_{0}}\in D}{\mathop{\sup }}\,{{\int }_{\mathbb{T}}}{{\left\| f\left( z \right)-f\left( {{z}_{0}} \right) \right\|}^{q}}{{P}_{{{z}_{0}}}}\left( z \right)dm\left( z \right)$$

holds for all trigonometric polynomials 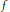$f$ with coefficients in $B$ if and only if $B$ admits an equivalent norm which is $q$-uniformly convex, where

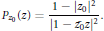$${{P}_{{{z}_{0}}}}\left( z \right)=\frac{1-|{{z}_{0}}{{|}^{2}}}{|1-{{{\bar{z}}}_{0}}z{{|}^{2}}}.$$

The validity of the converse inequality is equivalent to the existence of an equivalent $q$-uniformly smooth norm.

Keywords

46E4042B2546B20BMOCarleson measuresLusin typeLusin cotypeuniformly convex spacesuniformly smooth spaces
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 62 , Issue 4 , 01 August 2010 , pp. 827 - 844
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Blasco, O., Hardy spaces of vector-valued functions: duality. Trans. Amer. Math. Soc. 308(1988), no. 2, 495–507. doi:10.2307/2001088Google Scholar
[2] Blasco, O., Remarks on vector-valued B MOA and vector-valued multipliers. Positivity 4(2000), no. 4, 339–356. doi:10.1023/A:1009890316575Google Scholar
[3] Bourgain, J., Vector-valued singular integrals and the H1-B MO duality. In: Probability theory and harmonic analysis, Monogr. Textbooks Pure Appl. Math., 98, Dekker, New York, 1986, pp. 1–19.Google Scholar
[4] Coifman, R. R., Meyer, Y., and Stein, E. M., Some new function spaces and their applications to harmonic analysis. J. Funct. Anal. 62(1985), no. 2, 304–335. doi:10.1016/0022-1236(85)90007-2Google Scholar
[5] Garćıa-Cuerva, J. and Rubio de Francia, J. L., Weighted norm inequalities and related topics. North-Holland Mathematics Studies, 116, North-Holland Publishing Co., Amsterdam, 1985.Google Scholar
[6] Garnett, J. B., Bounded analytic functions. Pure and Applied Mathematics, 96, Academic Press Inc., New York–London, 1981.Google Scholar
[7] Kwapień, S., Isomorphic characterizations of inner product spaces by orthogonal series with vector valued coefficients. Studia Math. 44(1972), 583–595.Google Scholar
[8] Lindenstrauss, J. and Tzafriri, L., Classical Banach spaces. II. Function spaces. Results in Mathematics and Related Areas, 97, Springer-Verlag, Berlin–New York, 1979.Google Scholar
[9] Martınez, T., Torrea, J. L., and Xu, Q., Vector-valued Littlewood–Paley–Stein theory for semigroups. Adv. Math. 203(2006), no. 2, 430–475. doi:10.1016/j.aim.2005.04.010Google Scholar
[10] Pisier, G., Martingales with values in uniformly convex spaces. Israel J. Math. 20(1975), no. 3–4, 326–350. doi:10.1007/BF02760337Google Scholar
[11] Pisier, G., Probabilistic methods in the geometry of Banach spaces. In: Probability and analysis, Lecture Notes in Math., 1206, Springer, Berlin, 1986, pp. 167–241.Google Scholar
[12] Pisier, G., Factorization of linear operators and geometry of Banach spaces. CB MS Regional Conference Series in Mathematics, 60, American Mathematical Society, Providence, RI, 1986.Google Scholar
[13] Stein, E. M., Singular integrals and differentiability properties of functions. Princeton Mathematical Series, 30, Princeton University Press, Princeton, NJ, 1970.Google Scholar
[14] Stein, E. M., Harmonic analysis: real-variable methods, orthogonality, and oscillatory integrals. Princeton Mathematical Series, 43, Princeton University Press, Princeton, NJ, 1993.Google Scholar
[15] Xu, Q., Littlewood–Paley theory for functions with values in uniformly convex spaces. J. Reine Angew. Math. 504(1998), 195–226. doi:10.1515/crll.1998.107Google Scholar