No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
A surface of order three F in the real projective three-space P3 is met by every line, not in F, in at most three points. F is biplanar if it contains exactly one non-differentiable point v and the set of tangents of F at v is the union of two distinct planes, say τ1 and τ2.
In [2], we examined the biplanar surfaces containing the line τ1 ⌒ τ2. In the present paper, we classify and describe the biplanar F with the property that τ1 ⌒ τ2⌒ F = {v}.
We denote the planes, lines and points of P3 by the letters α, β, …, L, M, … and p, q, … respectively. For a collection of flats α, L, p, …, 〈α, L, p, …〉 denotes the flat of P3 spanned by them. For a set M in P3, 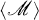 denotes the flat of P3 spanned by the points of
denotes the flat of P3 spanned by the points of 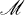 .
.