Hostname: page-component-f554764f5-nt87m Total loading time: 0 Render date: 2025-04-10T06:43:48.737Z Has data issue: false hasContentIssue false
  • English
  • Français

A Bipartitional Function Arising in Hall's Algebra

Published online by Cambridge University Press:  20 November 2018

I. J. Davies
I. J. Davies*
Affiliation:
University College, Swansea, Wales
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Hall's algebra (3) is an algebra over the field V(p) of rational functions in the indeterminate p with coefficients in the field V of complex numbers. The basis of the algebra consists of elements Gλ which are in one-one correspondence with the set of all partitions (λ) and whose multiplication "constants" are the "Hall polynomials" 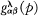, i-e.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 15 , 1963 , pp. 641 - 649
Copyright
Copyright © Canadian Mathematical Society 1963

References

1. Davies, I. J., Enumeration of certain subgroups of Abelian p-groups, Proc. Edinburgh Math. Soc. (2), Part 1, 13 (1962), 1–4.Google Scholar
2. Delsarte, S., Fonctions de Môbius sur les groupes abéliens finis, Ann. Math. (2), 49 (1948), 600–609.Google Scholar
3. Green, J. A., Les Polynotnes de Hall et les caractères des groupes GL(n, q), Colloque d'Algèbre Supérieure, Brussels (1956), 207-215.Google Scholar
4. Hall, P., Edinburgh Math. Soc. Coll., St. Andrews, 1955.Google Scholar
5. Kinosita, Y., On an enumeration of certain subgroups of a p-groupf J. Osaka Inst. Sci. Tech, Part I, 1 (1949), 13–20.Google Scholar
6. Kostka, C., Tafeln und Formeln fur symmetrische Functionen, Jahresb. d. deutschen Math.- Verein., 16 (1907), 429–450.Google Scholar
7. Littlewood, D. E., The theory of group characters and matrix representation of groups, 2nd ed. (Oxford Univ. Press, 1950), p. 87.Google Scholar
8. MacMahon, P. A., Combinatory analysis, Vol. 1 (Cambridge Univ. Press, 1915), p. 136.Google Scholar
9. MacMahon, P. A., Combinatory analysis, Vol. 2 (Cambridge Univ. Press, 1916), p. 10.Google Scholar
10. Riordan, J., An introduction to combinatorial analysis (New York, 1958), p. 153.Google Scholar
11. Sylvester, J. J., Collected mathematical papers, Vol. 4 (Cambridge Univ. Press, 1912), p. 10.Google Scholar
12. Yeh, Y., On prime power abelian groups, Bull. Amer. Math. Soc, 54 (1948), 323–327.Google Scholar