Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-01-24T13:15:16.235Z Has data issue: false hasContentIssue false
  • English
  • Français

Biorthogonal Systems in lp-Spaces

Published online by Cambridge University Press:  20 November 2018

R. Keown  and
C. Conatser
R. Keown
Affiliation:
University of Arkansas, Fayetteville, Arkansas
C. Conatser
Affiliation:
University of Illinois, Urbana, Illinois
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Our aim in this paper is to generalize certain ideas and results of Bary (1) on biorthogonal systems in separable Hilbert spaces to their counterparts in separable lp-spaces, 1 < p.The main result of Bary is to characterize a natural generalization of the concept of orthonormal basis for a Hilbert space. That of this paper is to characterize the concept of a Bary basis which is a generalization of the idea of standard basis of an lp-space. The result is interesting for lp-spaces because of the paucity of standard bases in these spaces.

Before summarizing our results, we shall introduce some notation and recall a few pertinent definitions and facts. The symbols 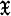and denote mutually conjugate lp-spaces, where 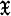is the space lt and the space lswith 1 < r <2 and 2 < s = r/(r – 1).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 625 - 638
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Bary, N. K., Biorthogonal systems and bases in Hilbert space, Ucen. Zap. 148 Matematika (1951), 69–107. (Russian)Google Scholar
2. Brauer, F., The completeness of biorthogonal systems, Michigan Math. J. 11 (1964), 379–383.Google Scholar
3. Gel'fand, I. M., A remark on the work of N. K. Bary: llBiorthogonal systems and bases in a Hilbert space”, Ucen. Zap. 148 Matematika (1951), 224–225. (Russian)Google Scholar
4. Keown, R., Some new Hilbert algebras, Trans. Amer. Math. Soc. 128 (1967), 71–87.Google Scholar
5. Keown, R., Reflexive Banach algebras, Proc. Amer. Math. Soc. 6 (1955), 252–259.Google Scholar
6. Levin, S. S., Ùber einige mit der Konvergenz im Mittel verbundenen Eigenschaften von Funktionenfolgen, Math. Z. 32 (1930), 491–511.Google Scholar
7. Pell, A., Biorthogonal systems of functions, Trans. Amer. Math. Soc. 12 (1911), 135–164.Google Scholar