Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T05:55:27.106Z Has data issue: false hasContentIssue false
  • English
  • Français

Bifurcations of Limit Cycles From Infinity in Quadratic Systems

Published online by Cambridge University Press:  20 November 2018

Lubomir Gavrilov  and
Iliya D. Iliev
Lubomir Gavrilov
Affiliation:
Laboratoire Ámile Picard, CNRS UMR 5580, Université Paul Sabatier, 118, route de Narbonne, 31062 Toulouse Cedex, France
Iliya D. Iliev
Affiliation:
Institute of Mathematics, Bulgarian Academy of Sciences, P.O. Box 373, 1090 Sofia, Bulgaria
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We investigate the bifurcation of limit cycles in one-parameter unfoldings of quadractic differential systems in the plane having a degenerate critical point at infinity. It is shown that there are three types of quadratic systems possessing an elliptic critical point which bifurcates from infinity together with eventual limit cycles around it. We establish that these limit cycles can be studied by performing a degenerate transformation which brings the system to a small perturbation of certain well-known reversible systems having a center. The corresponding displacement function is then expanded in a Puiseux series with respect to the small parameter and its coefficients are expressed in terms of Abelian integrals. Finally, we investigate in more detail four of the cases, among them the elliptic case (Bogdanov-Takens system) and the isochronous center 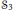${{\mathcal{S}}_{3}}$. We show that in each of these cases the corresponding vector space of bifurcation functions has the Chebishev property: the number of the zeros of each function is less than the dimension of the vector space. To prove this we construct the bifurcation diagram of zeros of certain Abelian integrals in a complex domain.

Keywords

34C0734C0534C10
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 54 , Issue 5 , 01 October 2002 , pp. 1038 - 1064
Copyright
Copyright © Canadian Mathematical Society 2002

References

[1] Chicone, C. and Jacobs, M., Bifurcations of limit cycles from quadratic isochrones. J. Differential Equations 91 (1991), 268–326.Google Scholar
[2] Chow, Shui-Nee, Li, Chengzhi and Yi, Yingfei, The cyclicity of period annulus of degenerate quadratic Hamiltonian system with elliptic segment. National Univ. of Singapore, 2000, preprint.Google Scholar
[3] Gavrilov, L., The infinitesimal 16th Hilbert problem in the quadratic case. Invent.Math. 143 (2001), 449–497.Google Scholar
[4] Gavrilov, L. and Iliev, I. D., Second order analysis in polynomially perturbed reversible quadratic Hamiltonian systems. Ergodic Theory Dynamical Systems 20(2000) 1671–1686.Google Scholar
[5] Maoan, Han, Ye, Yanqian and Zhu, Deming, Cyclicity of homoclinic loops and degenerate cubic Hamiltonians. Sci. China Ser. A (6) 42 (1999), 605–617.Google Scholar
[6] Horozov, E. and Iliev, I. D., On the number of limit cycles in perturbations of quadratic Hamiltonian systems. Proc. LondonMath. Soc. 69 (1994), 198–224.Google Scholar
[7] Iliev, I. D., Higher order Melnikov functions for degenerate cubic Hamiltonians. Adv. Differential Equations (4) 1 (1996), 689–708.Google Scholar
[8] Iliev, I. D., Perturbations of quadratic centers. Bull. Sci. Math. 22 (1998), 107–161.Google Scholar
[9] Ince, E. L., Ordinary Differential Equations. Dover, New York, 1956.Google Scholar
[10] Li, Bao-yi and Zhang, Zhi-fen, A note on a result of G. S. Petrov about the weakened 16th Hilbert problem. J. Math. Anal. Appl. 190 (1995), 489–516.Google Scholar
[11] Mardešić, P., The number of limit cycles of polynomial deformations of a Hamiltonian vector field. Ergodic Theory Dynamical Systems Theory 10 (1990), 523–529.Google Scholar
[12] Petrov, G. S., On the number of zeros of complete elliptic integrals. Functional Anal. Appl. 18 (1984), 73–74.Google Scholar
[13] Petrov, G. S., Elliptic integrals and their nonoscillation. Functional Anal. Appl. 20 (1986), 37–40.Google Scholar
[14] Roussarie, R., Bifurcations of Planar Vector Fields and Hilbert's sixteenth Problem. Progr. Math. 164, Birkhäuser, Basel, 1998.Google Scholar
[15] Shafer, Douglas S. and Zegeling, A., Bifurcation of limit cycles from quadratic centers. J. Differential Equations (1) 122 (1995), 48–70.Google Scholar
[16] Yanqian, Ye, Theory of limit cycles. Transl. Math. Monogr., Amer. Math. Soc. 66(1986).Google Scholar
[17] Zegeling, A. and Kooij, R. E., The distribution of limit cycles in quadratic systems with four finite singularities. J. Differential Equations 151 (1999), 373–385.Google Scholar
[18] Zhao, Yulin, Liang, Zhaojun and Lu, Gang, The cyclicity of the period annulus of the quadratic Hamiltonian systems with non-Morsean point. J. Differential Equations 162 (2000), 199–223.Google Scholar
[19] Zhao, Yulin and Zhu, Siming, Perturbations of the non-generic quadratic Hamiltonian vector fields with hyperbolic segment. Bull. Sci. Math. (2) 125 (2001), 109–138.Google Scholar
[20] Żołądek, H., Quadratic systems with center and their perturbations. J. Differential Equations (2) 109 (1994), 223–273.Google Scholar