Article contents
Basic Objects for an Algebraic Homotopy Theory
Published online by Cambridge University Press: 20 November 2018
Extract
The purposes of this paper are:
(A) To show (§§ 1, 3, 5) that some of the usual notions of homotopy theory (sums, quotients, suspensions, loop functors) exist in the category 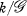 of affine k-schemes where the affine rings are countably generated.
of affine k-schemes where the affine rings are countably generated.
(B) By example to demonstrate some of the more geometric relations between two objects of 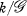 and their quotient or to study the algebraic suspension of one of them. See §§ 2.1, 2.2, 2.3, 3.
and their quotient or to study the algebraic suspension of one of them. See §§ 2.1, 2.2, 2.3, 3.
(C) To prove (§4) that the algebraic suspension (in R/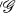 ) of the n-sphere is homeomorphic to the n + 1 sphere for the usual topologies.
) of the n-sphere is homeomorphic to the n + 1 sphere for the usual topologies.
(D) To show that the algebraic loop functor is right adjoint to the algebraic suspension functor (§5).
These results can be viewed as a precursor of definitions for an algebraic homotopy theory from a “geometric” point of view (rather than a more algebraic standpoint employing Galois theory [5]).
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1972
References
- 2
- Cited by


