Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-14T07:25:29.531Z Has data issue: false hasContentIssue false
  • English
  • Français

AV-Courant Algebroids and Generalized CR Structures

Published online by Cambridge University Press:  20 November 2018

David Li-Bland
David Li-Bland*
Affiliation:
Department of Mathematics, University of Toronto, Toronto, ON, M5S 2E4 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

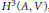We construct a generalization of Courant algebroids that are classified by the third cohomology group ${{H}^{3}}(A,\,V)$, where 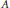$A$ is a Lie Algebroid, and 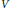$V$ is an 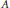$A$-module. We see that both Courant algebroids and 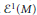${{\text{ }\!\!\varepsilon\!\!\text{ }}^{1}}(M)$ structures are examples of them. Finally we introduce generalized 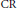$\text{CR}$ structures on a manifold, which are a generalization of generalized complex structures, and show that every 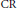$\text{CR}$ structure and contact structure is an example of a generalized 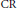$\text{CR}$ structure.

Keywords

53D18
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 63 , Issue 4 , 01 August 2011 , pp. 938 - 960
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Audin, M., da Silva, A. C., and Lerman, E., Symplectic geometry of integrable Hamiltonian systems. Lectures delivered at the Euro Summer School held in Barcelona, July 10–15, 2001. Advanced Courses in Mathematics, CRM Barcelona, Birkhäuser Verlag, Basel, 2003.Google Scholar
[2] Bressler, P. and Chervov, A., Courant algebroids. Geometry J. Math. Sci. 128(2005), no. 4, 3030–3053. doi:10.1007/s10958-005-0251-7Google Scholar
[3] Chen, Z. and Liu, Z.-J., Omni-Lie alegebroids. J. Geom. Phys. 60(2010), no. 5, 799–808. doi:10.1016/j.geomphys.2010.01.007Google Scholar
[4] Chen, Z., Liu, Z.-J., and Sheng, Y.-H., Dirac structures of omni-Lie algebroids. arXiv:0802.3819v2 [math.DG].Google Scholar
[5] Chen, Z., E-Courant algebroids. arXiv:0805.4093v2 [math.DG].Google Scholar
[6] Courant, T. and Weinstein, A., Beyond Poisson structures. In: Action hamiltoniennes de groupes. Troisième théorème de Lie (Lyon, 1986), Travaux en Cours, 27, Hermann, Paris, 1988, pp. 39–49.Google Scholar
[7] Courant, T. Dirac manifolds. Trans. Amer. Math. Soc. 319(1990), no. 2, 631–661. doi:10.2307/2001258Google Scholar
[8] Crainic, M. and Fernandes, R. L., Integrability of Lie brackets. Ann. of Math. 157(2003), no. 2, 575–620. doi:10.4007/annals.2003.157.575Google Scholar
[9] da Silva, A. C. and Weinstein, A., Geometric models for noncommutative algebras. Berkeley Mathematical Lecture Notes, 10, American Mathematical Society, Providence, RI, 2000.Google Scholar
[10] Grabowski, J. and Marmo, G., The graded Jacobi algebras and (co)homology. J. Phys. A 36(2003), no. 1, 161–181. doi:10.1088/0305-4470/36/1/311Google Scholar
[11] Guedira, F. and Lichnerowicz, A., Géometrie des algèbres de Lie locales de Kirillov. J. Math. Pures Appl. 63(1984), 407–484.Google Scholar
[12] Gualtieri, M., Generalized complex geometry. arXiv:math/0703298v2 [math.DG].Google Scholar
[13] Hitchin, N., Generalized Calabi-Yau manifolds. Q. J. Math. 54(2003), no. 3, 281–308. doi:10.1093/qmath/hag025Google Scholar
[14] Iglesias-Ponte, D. and Wade, A., Contact manifolds and generalized complex structures. J. Geom. Phys. 53(2005), no. 3, 249–258. doi:10.1016/j.geomphys.2004.06.006Google Scholar
[15] Iglesias-Ponte, D. and Wade, A., Integration of Dirac-Jacobi structures. J. Phys. A 39(2006), no. 16, 4181–4190. doi:10.1088/0305-4470/39/16/006Google Scholar
[16] Kirillov, A. A., Local Lie algebras. (Russian) Uspehi Mat. Nauk 31(1976), no. 4(190), 57–76.Google Scholar
[17] Lindström, U., Minasian, R., Tomasiello, A., and Zabzine, M., Generalized complex manifolds and supersymmetry. Comm. Math. Phys. 257(2005), no. 1, 235–256. doi:10.1007/s00220-004-1265-6Google Scholar
[18] Mackenzie, K., General theory of Lie groupoids and Lie algebroids. London Mathematical Society Lecture Note Series, 213, Cambridge University Press, Cambridge, 2005.Google Scholar
[19] Mackenzie, K. C. H. and Xu, P., Integration of Lie bialgebroids. Topology 39(2000), no. 3, 445–467. doi:10.1016/S0040-9383(98)00069-XGoogle Scholar
[20] Marle, C.-M., The Schouten-Nijenhuis bracket and interior products. J. Geom. Phys. 23(1997), no. 3–4, 350–359. doi:10.1016/S0393-0440(97)80009-5Google Scholar
[21] Marle, C.-M., On Jacobi manifolds and Jacobi bundles. In: Symplectic geometry, groupoids, and integrable systems (Berkeley, CA, 1989), Math. Sci. Res. Inst. Publ., 20, Springer, New York, 1991, pp. 227–246.Google Scholar
[22] Moerdijk, I. and Mrcun, J., On integrability of infinitesimal actions. Amer. J. Math. 124(2002), no. 3, 567–593. doi:10.1353/ajm.2002.0019Google Scholar
[23] Nunes da Costa, J. M. and Clemente-Gallardo, J., Dirac structures for generalized Lie bialgebroids. J. Phys. A 37(2004), no. 7, 2671–2692. doi:10.1088/0305-4470/37/7/011Google Scholar
[24] Severa, P. and Weinstein, A., Poisson geometry with a 3-form background. Prog. Theor. Phys. Suppl. 144(2001), 145–154.Google Scholar
[25] Shiga, K., Cohomology of Lie algebras over a manifold I. J. Math Soc. Japan 26(1974), 324–61. doi:10.2969/jmsj/02620324Google Scholar
[26] Vaisman, I., Generalized CRF-structures. Geom. Dedicata 133(2008), 129–154. doi:10.1007/s10711-008-9239-zGoogle Scholar
[27] Wade, A., Conformal Dirac structures. Lett. Math. Phys. 53(2000), no. 4, 331–348. doi:10.1023/A:1007634407701Google Scholar