Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-08T08:14:37.376Z Has data issue: false hasContentIssue false
  • English
  • Français

Automorphism Groups of Unary Algebras on Groups

Published online by Cambridge University Press:  20 November 2018

G. H. Wenzel
G. H. Wenzel*
Affiliation:
Queen's University, Kingstony Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper presents a systematic study of the automorphism groups of those unary (universal) algebras 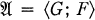whose carrier set G is the carrier set of some group 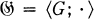) and whose automorphism set 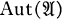contains the right translations of the latter group. These algebras appear, apart from the known classical contexts, repeatedly in characterization theorems of endomorphism semigroups (End) and automorphism groups (Aut) of algebras due to Grätzer (3; 4; 5), Makkai (7), Armbrust and Schmidt (1), Birkhoff (2), and others.

Our main result (Theorem 1) constitutes an essential strengthening of a theorem of Birkhoff and represents the automorphism group 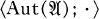of a unary algebra 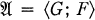(where F is contained in the set 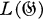of left translations of the group 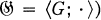as wreath product of two groups that are easily determined from F and G.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 1165 - 1171
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Armbrust, M. and Schmidt, J., Zum Cayleyschen Darstellungssatz, Math. Ann. 154 (1964), 70–72.Google Scholar
2. Birkhoff, G., Lattice theory, rev. éd., Amer. Math. Soc. Colloq. Publ., Vol. 25 (Amer. Math. Soc, Providence, R.I., 1948).Google Scholar
3. Gràtzer, G., On the endomorphism semigroup of simple algebras, Math. Ann. 170 (1967), 334–338.Google Scholar
4. Gràtzer, G., Universal algebra, The University Series in Higher Mathematics (Van Nostrand, Princeton, N.J., 1968).Google Scholar
5. Gràtzer, G., Some results on universal algebras, Mimeographed notes, 1962.Google Scholar
6. Hall, M., The theory of groups (Macmillan, New York, 1959).Google Scholar
7. Makkai, M., Solution of a problem of G. Gràtzer concerning endomorphism semigroups, Acta Math. Acad. Sci. Hungar. 15 (1964), 297–307.Google Scholar