Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-25T18:44:19.577Z Has data issue: false hasContentIssue false
  • English
  • Français

Autometrization and the SymmetricDifference

Published online by Cambridge University Press:  20 November 2018

J. G. Elliott
J. G. Elliott*
Affiliation:
Michigan State College
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The fact that the symmetric difference 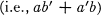is a group operation in a Boolean algebra is, of course, well known. Not so well known is the fact observed by Ellis [3] that it possesses some of the desirable properties of a metric distance function. Specifically, if * denotes this operation, it is easy to verify that

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 5 , 1953 , pp. 324 - 331
Copyright
Copyright © Canadian Mathematical Society 1953

References

1. Bernstein, B. A., Operations with respect to which the elements of a Boolean algebra form a group, Trans. Amer. Math. Soc, 26 (1924), 171–175.Google Scholar
2. Bernstein, B. A., On the existence of fields in Boolean algebras, Trans. Amer. Math. Soc, 84 (1928), 654–657.Google Scholar
3. Ellis, D., Autometrized Boolean algebras I, Can. J. Math., 3 (1951), 87–93.Google Scholar
4. Ellis, D., Geometry in abstract distance spaces (Debrecen, Hungary, 1951), 3.Google Scholar
5. Frink, O., On the existence of linear algebras in Boolean algebras, Bull. Amer. Math. Soc, 34 (1928), 329–333.Google Scholar
6. Gleason, A. M., A note on a theorem of Helson, Colloquium Mathematicum, 2 (1949), 5–6.Google Scholar
7. Helson, H., On the symmetric difference of sets as a group operator, Colloquium Mathematicum, 1 (1948), 203–205.Google Scholar
8. Marczewski, E., Concerning the symmetric difference in the theory of sets and in Boolean algebras, Colloquium Mathematicum, 1 (1948), 199–202.Google Scholar