Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T06:02:43.300Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotical Behaviour of Roots of Infinite Coxeter Groups

Published online by Cambridge University Press:  20 November 2018

Christophe Hohlweg ,
Jean-Philippe Labbé  and
Vivien Ripoll
Christophe Hohlweg
Affiliation:
Université du Québec à Montréal,LaCIM et Département de Mathématiques, Montréal, Québec, H3C 3P8. e-mail: [email protected]@lacim.ca
Jean-Philippe Labbé
Affiliation:
Freie Universität Berlin, Institut für Mathematik, 14195, Berlin, Deutschland. e-mail: [email protected]
Vivien Ripoll
Affiliation:
Université du Québec à Montréal,LaCIM et Département de Mathématiques, Montréal, Québec, H3C 3P8. e-mail: [email protected]@lacim.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

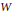Let $W$ be an infinite Coxeter group. We initiate the study of the set $E$ of limit points of “normalized” roots (representing the directions of the roots) of 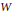$\text{W}$. We show that $E$ is contained in the isotropic cone 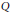$Q$ of the bilinear form 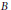$B$ associated with a geometric representation, and we illustrate this property with numerous examples and pictures in rank 3 and 4. We also define a natural geometric action of 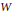$W$ on $E$, and then we exhibit a countable subset of $E$, formed by limit points for the dihedral reflection subgroups of 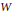$W$. We explain how this subset is built fromthe intersection with 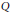$Q$ of the lines passing through two positive roots, and finally we establish that it is dense in $E$.

Keywords

17B2220F55Coxeter grouprootsroot systemlimit pointaccumulation set
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 66 , Issue 2 , 01 April 2014 , pp. 323 - 353
Copyright
Copyright © Canadian Mathematical Society 2014

References

[BB05] Björner, A. and Brenti, F., Combinatorics of Coxeter groups. Graduate Texts in Mathematics, 231, Springer, New York, 2005.Google Scholar
[BD10] Bonnafé, C. and Dyer, M. J., Semidirect product decomposition of Coxeter groups. Comm. Algebra 38(2010), no. 4, 1549–1574. http://dx.doi.org/10.1080/00927870902980354 Google Scholar
[BH93] Brink, B. and Howlett, R. B., A finiteness property and an automatic structure for Coxeter groups. Math. Ann. 296(1993), no. 1, 179–190. http://dx.doi.org/10.1007/BF01445101 Google Scholar
[Bou68] Bourbaki, N., Élements de mathématique. Fasc. XXXIV. Groupes et algèbres de Lie. Chapitres 4–6, Hermann, Paris, 1968.Google Scholar
[Deo89] Deodhar, V. V., A note on subgroups generated by reflections in Coxeter groups. Arch. Math. (Basel) 53(1989), no. 6, 543–546. http://dx.doi.org/10.1007/BF01199813 Google Scholar
[Dye90] Dyer, M., Reflection subgroups of Coxeter systems. J. Algebra 135(1990), no. 1, 57–73. http://dx.doi.org/10.1016/0021-8693(90)90149-I Google Scholar
[Dye10] Dyer, M., On rigidity of abstract root systems of Coxeter systems. arxiv:1011.2270, 2010. Google Scholar
[Dye11] Dyer, M., On the weak order of Coxeter groups. arxiv:1108.5557, 2011.Google Scholar
[Dye12] Dyer, M., Imaginary cone and reflection subgroups of Coxete[BB05] A. Björner and F. Brenti, Combinatorics of Coxeter groups. Graduate Texts in Mathematics, 231, Springer, New York, 2005.Google Scholar
[BD10] Bonnafé, C. and Dyer, M. J., Semidirect product decomposition of Coxeter groups. Comm. Algebra 38(2010), no. 4, 1549–1574. http://dx.doi.org/10.1080/00927870902980354 Google Scholar
[BH93] Brink, B. and Howlett, R. B., A finiteness property and an automatic structure for Coxeter groups. Math. Ann. 296(1993), no. 1, 179–190. http://dx.doi.org/10.1007/BF01445101/ Google Scholar
[Bou68] Bourbaki, N., Élements de mathématique. Fasc. XXXIV. Groupes et algèbres de Lie. Chapitres 4–6, Hermann, Paris, 1968.Google Scholar
[Deo89] Deodhar, V. V., A note on subgroups generated by reflections in Coxeter groups. Arch. Math. (Basel) 53(1989), no. 6, 543–546. http://dx.doi.org/10.1007/BF01199813 Google Scholar
[Dye90] Dyer, M., Reflection subgroups of Coxeter systems. J. Algebra 135(1990), no. 1, 57–73. http://dx.doi.org/10.1016/0021-8693(90)90149-I Google Scholar
[Dye10] Dyer, M., On rigidity of abstract root systems of Coxeter systems. arxiv:1011.2270, 2010.Google Scholar
[Dye11] Dyer, M., On the weak order of Coxeter groups. arxiv:1108.5557, 2011.Google Scholar
[Dye12] Dyer, M., Imaginary cone and reflection subgroups of Coxeter groups. arxiv:1210.5206, 2012. Google Scholar
[DHR13] Dyer, M., Hohlweg, C., and Ripoll, V., Imaginary cones and limit roots of infinite Coxeter groups. arxiv:1303.6710, 2013. Google Scholar
[Fu12] Fu, X., The dominance hierarchy in root systems of Coxeter groups. J. Algebra 366(2012), 187–204. http://dx.doi.org/10.1016/j.jalgebra.2012.05.013 Google Scholar
[Fu13] Fu, X., Coxeter groups, imaginary cones and dominance. Pacific J. Math. 262(2013), no. 2, 339–363. http://dx.doi.org/10.2140/pjm.2013.262.339 Google Scholar
[HMN12] Higashitani, A., Mineyama, R., and Nakashima, N., A metric analysis of infinite Coxeter groups : the case of type (n − 1; 1) Coxeter matrices. arxiv:1212.6617, April 2013.Google Scholar
[How96] Howlett, R. B., Introduction to Coxeter groups. Lectures at A.N.U. Geometric Group Theory Workshop, 1996. http://www.maths.usyd.edu.au/res/Algebra/How/1997-6.html. Google Scholar
[Hum90] Humphreys, J. E., Reflection groups and Coxeter groups. Cambridge Studies in Advanced Mathematics, 29, Cambridge University Press, Cambridge, 1990.Google Scholar
[Kac90] Kac, V. G., Infinite-dimensional Lie algebras. Third ed., Cambridge University Press, Cambridge, 1990. http://dx.doi.org/10.1017/CBO9780511626234 Google Scholar
[Kan01] Kane, R., Reflection groups and invariant theory. CMS Books in Mathematics/Ouvrages de Mathématiques de la SMC, 5, Springer-Verlag, New York, 2001.Google Scholar
[Kra09] Krammer, D., The conjugacy problem for Coxeter groups. Groups Geom. Dyn. 3(2009), no. 1, 71–171. http://dx.doi.org/10.4171/GGD/52 Google Scholar
[LN04] Loos, O. and Neher, E., Locally finite root systems. Mem. Amer. Math. Soc. 171(2004), no. 811.Google Scholar
[MP89] Moody, R. V. and Pianzola, A., On infinite root systems. Trans. Amer. Math. Soc. 315(1989), no. 2, 661–696. http://dx.doi.org/10.1090/S0002-9947-1989-0964901-8 Google Scholar
[Sau91] Saunders, C., The reflection representations of some Chevalley groups. J. Algebra 137(1991), no. 1, 145–165. http://dx.doi.org/10.1016/0021-8693(91)90085-M Google Scholar
[S+13] Stein, W. A. et al., Sage Mathematics Software (Version 5.9). The Sage Development Team, 2013. http://www.sagemath.org. Google Scholar
[Vin71] Vinberg, È.B., Discrete linear groups that are generated by reflections. Izv. Akad. Nauk SSSR Ser. Mat. 35(1971), 1072–1112.Google Scholar