Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-28T03:03:56.850Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic Transformations of q-Series

Published online by Cambridge University Press:  20 November 2018

Richard J. McIntosh
Richard J. McIntosh*
Affiliation:
Department of Mathematics and Statistics University of Regina Regina, SK S4S 0A2, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For the $q$-series 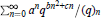$\sum\nolimits_{n=0}^{\infty }{{{a}^{n}}{{q}^{b{{n}^{2}}+cn}}/}\,{{(q)}_{n}}$ we construct a companion $q$-series such that the asymptotic expansions of their logarithms as 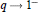$q\,\to \,{{1}^{-}}$ differ only in the dominant few terms. The asymptotic expansion of their quotient then has a simple closed form; this gives rise to a new $q$–hypergeometric identity. We give an asymptotic expansion of a general class of $q$-series containing some of Ramanujan's mock theta functions and Selberg's identities.

Keywords

11B6533D1034E0541A60
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 50 , Issue 2 , 01 April 1998 , pp. 412 - 425
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Andrews, G.E., q-identities of Auluck, Carlitz, and Rogers. Duke Math. J. 33(1966), 575–581.Google Scholar
2. Andrews, G.E., The Theory of Partitions. Addison-Wesley, Reading, 1976.Google Scholar
3. Andrews, G.E., q-Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra. CBMS conference series 66, Amer. Math. Soc., Providence, Rhode Island, 1986.Google Scholar
4. Andrews, G.E., The fifth and seventh order mock theta functions. Trans. Amer.Math. Soc. 293(1986), 113–134.Google Scholar
5. Andrews, G.E., Mock theta functions. Proc. Sympos. Pure Math. 49(1989), 283–298.Google Scholar
6. Apostol, T. M., Modular Functions and Dirichlet Series in Number Theory. Second edition, Springer-Verlag, New York, 1990.Google Scholar
7. Bellman, R., A Brief Introduction to Theta Functions. Holt, Rinehart and Winston, New York, 1961.Google Scholar
8. Hardy, G.H. and Wright, E.M., An Introduction to the Theory of Numbers. Fourth edition, Oxford University Press, London, 1960.Google Scholar
9. Lewin, L., Polylogarithms and Associated Functions. North-Holland, New York, 1981.Google Scholar
10. Lewin, L., A large symbolic manipulation program developed at the University of Waterloo. MAPLE is a registered trademark of Waterloo Maple Soltware.Google Scholar
11. McIntosh, R.J., Some asymptotic formulae for q-hypergeometric series. J. LondonMath. Soc. (2) 51(1995), 120–136.Google Scholar
12. Ramanujan, S., Collected Papers. Cambridge University Press, 1927. reprinted by Chelsea, New York, 1962.Google Scholar
13. Ramanujan, S., The Lost Notebook and Other Unpublished Papers. Narosa, New Delhi, 1988.Google Scholar
14. Selberg, A., Über die Mock-Thetafunktionen siebenter 0rdnung. Arch.Math. og Naturvidenskab 41(1938), 3–15.Google Scholar
15. Watson, G.N., The final problem: an account of the mock theta functions. J. London Math. Soc. 11(1936), 55–80.Google Scholar
16. Watson, G.N., The mock theta functions (2). Proc. London Math. Soc. (2) 42(1937), 274–304.Google Scholar