Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T19:04:31.708Z Has data issue: false hasContentIssue false
  • English
  • Français

Association Schemes for Ordered Orthogonal Arrays and (T, M, S)-Nets

Published online by Cambridge University Press:  20 November 2018

W. J. Martin  and
D. R. Stinson
W. J. Martin
Affiliation:
Mathematics and Statistics, University of Winnipeg, Winnipeg, Manitoba R3B 2E9 email: [email protected]
D. R. Stinson
Affiliation:
Combinatorics and Optimization, University of Waterloo, Waterloo, Ontario, N2L 3G1 email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

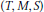In an earlier paper [10], we studied a generalized Rao bound for ordered orthogonal arrays and $(T,\,M,\,S)$-nets. In this paper, we extend this to a coding-theoretic approach to ordered orthogonal arrays. Using a certain association scheme, we prove a MacWilliams-type theorem for linear ordered orthogonal arrays and linear ordered codes as well as a linear programming bound for the general case. We include some tables which compare this bound against two previously known bounds for ordered orthogonal arrays. Finally we show that, for even strength, the 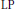$\text{LP}$ bound is always at least as strong as the generalized Rao bound.

Keywords

05B1505E3065C99
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 51 , Issue 2 , 01 April 1999 , pp. 326 - 346
Copyright
Copyright © Canadian Mathematical Society 1999

References

[1] Adams, M. J., Generalized Orthogonal Arrays and Related Structures. Ph.D. thesis, Department of Mathematics, University of Wyoming, Laramie, Wyoming, May 1997.Google Scholar
[2] Brouwer, A. E., Cohen, A. M. and Neumaier, A., Distance-Regular Graphs. Springer-Verlag, Berlin, 1989.Google Scholar
[3] Clayman, A. T., Lawrence, K. M., Mullen, G. L., Niederreiter, H. and Sloane, N. J. A., Updated tables of parameters of (T;M; S)-nets. J. Combin. Des., to appear.Google Scholar
[4] Delsarte, P., An algebraic approach to the association schemes of coding theory. Philips Res. Rep. Suppl. 10 (1973).Google Scholar
[5] Godsil, C. D., Algebraic Combinatorics. Chapman and Hall, New York, 1993.Google Scholar
[6] Godsil, C. D., MacWilliams theorem for product schemes. Preprint.Google Scholar
[7] Lawrence, K.M., A combinatorial interpretation o. (t;m; s)-nets in base b. J. Combin. Des. 4 (1996), 275–293.Google Scholar
[8] Martin, W. J., Designs in product association schemes. Designs, Codes and Cryptography, 16 (1999) 271–289.Google Scholar
[9] Martin, W. J., Linear programming bounds for ordered orthogonal arrays and (t;m; s)-nets. Proceedings of the Third International Conference on Monte Carlo and Quasi-Monte Carlo Methods in Scientific Computing. Lect. Notes Comput. Sci. Eng., Springer-Verlag, to appear.Google Scholar
[10] Martin, W. J. and Stinson, D. R., A generalized Rao bound for ordered orthogonal arrays and (t;m; s)-nets. Canad. Math. Bull., to appear.Google Scholar
[11] Mullen, G. L. and Whittle, G., Point sets with uniformity properties and orthogonal hypercubes. Monatsh. Math. 113 (1992), 265–273.Google Scholar
[12] Mullen, G. L., Mahalanabis, A. and Niederreiter, H., Tables of(T; M; S)-net and (T; S)-sequence parameters. In: Monte Carlo and Quasi-Monte Carlo Methods in Scientific Computing (eds. Niederreiter, H. and Shiue, P.), Lecture Notes in Statist. 106, Springer, New York, 1995, pp. 58–86.Google Scholar
[13] Niederreiter, H., Point sets and sequences with small discrepancy. Monatsh.Math. 104 (1987), 273–337.Google Scholar
[14] Rosenbloom, M. Yu. and Tsfasman, M. A., Codes for the m-metric. Problems Inform. Transmission (1) 33 (1997), 45–52.Google Scholar
[15] Schmid, W. Ch., (t;m; s)-nets: Digital Constructions and Combinatorial Aspects. Ph.D. thesis, Institute of Mathematics, University of Salzburg, Salzburg, Austria, May 1995.Google Scholar
[16] Yamamoto, S., Fujii, Y. and Hamada, N., Computation of some series of association algebras. J. Sci. Hiroshima University (2) 29 (1965), 181–215.Google Scholar