Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-12-02T20:38:31.681Z Has data issue: false hasContentIssue false
  • English
  • Français

The Ascending and Descending Varietal Chains of a Variety

Published online by Cambridge University Press:  20 November 2018

B. Jónsson ,
G. McNulty  and
R. Quackenbush
B. Jónsson
Affiliation:
Vanderbilt University, Nashville, Tennessee
G. McNulty
Affiliation:
Dartmouth College, Hanover, New Hampshire
R. Quackenbush
Affiliation:
University of Manitoba, Winnipeg, Manitoba
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let F be a variety (equational class) of algebras. For n ≧ 0, Vn is the variety generated by the F-free algebra on n free generators while Vn is the variety of all algebras satisfying each identity of V which has no more than n variables. (Equivalently, Vn is the class of all algebras, 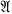, such that every n-generated subalgebra of 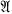is in V.) Note that unless nullary operation symbols are specified by the similarity type of V, V0 is the variety of all one element algebras while V° is the variety of all algebras.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 27 , Issue 1 , 01 February 1975 , pp. 25 - 31
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Evans, T., Identities and relations in commutative Moufang l∞ps (preprint).Google Scholar
2. Gupta, N. and Levin, F., Generating groups of certain soluble varieties, J. Austral. Math. Soc. (to appear).Google Scholar
3. Gupta, N., Levin, F., and Rhemtulla, A., Chains of varieties, Can. J. Math. 26 (1974), 190–206.Google Scholar
4. Jonsson, B., Algebras whose congruence lattices are distributive, Math. Scand. 21 (1967), 110–121.Google Scholar
5. Neumann, H., Varieties of groups (Springer-Verlag, Berlin, 1967).Google Scholar