Article contents
Are Non-Commutative Lp Spaces Really Non-Commutative?
Published online by Cambridge University Press: 20 November 2018
Extract
1. The central objects in integration theory can be considered to be an abelian Von Neumann algebra, L∞, of the measure space, together with a (not necessarily finite-valued) positive linear functional on it, the integral (see [10]). It is natural, therefore, to attempt to construct a “non-commutative” integration theory starting with a non-abelian Von Neumann algebra. Segal [9] and Dixmier [2] have developed such a theory, and constructed the Non-Commutative Lp spaces associated with a Von Neumann algebra M and a normal, faithful, semifinite trace (i.e. a unitarily invariant weight) t on M. They show that there exists a unique ultra-weakly dense *-ideal J of M such that t (extends to) a positive linear form on J . A generalisation of the Hölder inequality then shows that, for 1 ≦ p < ∞, the function
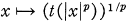
is a norm on J, denoted by || • ||p.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1981
References
- 3
- Cited by


