Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-12-04T09:26:28.236Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximation Harmonique Sur Les Surfaces de Riemann

Published online by Cambridge University Press:  20 November 2018

A. Boivin  and
P. M. Gauthier
A. Boivin
Affiliation:
Université de Montréal, Montréal, Québec
P. M. Gauthier
Affiliation:
Université de Montréal, Montréal, Québec
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Dans le présent article, surface de Riemann ou plus simplement surface désignera une variété analytique complexe R, connexe, sans bord et de dimension 1. En terme d'une variable locale, une fonction harmonique h, définie sur R, possédant une singularité isolée au point z0, peut s'écrire comme la somme d'une fonction harmonique

et d'une partie singulière

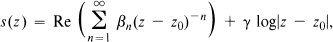
avec αn, βn ∈ C, γ ∈ R; les deux séries sont supposées convergentes, la première pour |z – z0| suffisamment petit, la seconde pour tout z ≠ z0. Alors h(z) = u(z) + s(z). Nous dirons que la singularité de h est non-essentielle si s(z) est de la forme

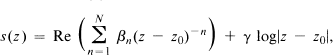
et newtonienne ou logarithmique si elle s'écrit

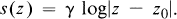
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 36 , Issue 1 , 01 February 1984 , pp. 1 - 8
Copyright
Copyright © Canadian Mathematical Society 1984

References

Bibliographie

1. Ahlfors, L. V. et Sario, L., Riemann surfaces (Princeton University Press, 1960).CrossRefGoogle Scholar
2. Bochner, S., Fortsetzung Riemannscher Flachen, Math. Ann. 98 (1928), 406–421.Google Scholar
3. Gauthier, P. M., Goldstein, M. et Ow, W. H., Uniform approximation on unbounded sets by harmonie functions with logarithmic singularities, Trans. Amer. Math. Soc. 261 (1980), 169–183.Google Scholar
4. Gauthier, P. M. et Hengartner, W., Approximation qualitative sur des ensembles non bornés. Sém. Math. Sup. 1981 (Les Presses de l'Université de Montréal, 1982).Google Scholar
5. Hurwitz, A., Allgemeine Funktionentheorie und Elliptische Funktionen. Mit einem Abschnitt von R. Courant. Mit einem Anhang von H. Röhrl, 4 Aufl. (Springer-Verlag, Berlin-Gôttingen-Heidelberg-New York, 1964).Google Scholar
6. Pfluger, A., Ein Approximationsatz für harmonische Funktionen auf Riemannschen Flächen, Ann. Acad. Sci. fenn., Ser. A, 1, 216 (1956).Google Scholar
7. Pfluger, A., Théorie der Riemannschen Flàchen (Springer-Verlag, Berlin-Gôttingen-Heidelberg, 1957).CrossRefGoogle Scholar
8. Rodin, B. et Sario, L., Convergence of normal operators, Ködai Math. Sem. Rep. 19 (1967), 165–175.Google Scholar
9. Rodin, B. et Sario, L., Principal functions (D. Van Nostrand, Princeton, N.J., 1968).CrossRefGoogle Scholar
10. Scheinberg, S., Uniform approximation by meromorphic functions having prescribed poles, Math. Ann. 243 (1979), 83–93.Google Scholar
11. Scheinberg, S., Gauthier's localization theorem on meromorphic uniform approximation, Pacific J. Math 707 (1983), 223–228.Google Scholar