Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-18T21:50:44.404Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximation and Similarity Classification of Stably Finitely Strongly Irreducible Decomposable Operators

Published online by Cambridge University Press:  20 November 2018

He Hua ,
Dong Yunbai  and
Guo Xianzhou
He Hua
Affiliation:
Department of Mathematics, Hebei University of Technology, Tianjin 300130, P.R. China, e-mail: [email protected], [email protected], [email protected]
Dong Yunbai
Affiliation:
Department of Mathematics, Hebei University of Technology, Tianjin 300130, P.R. China, e-mail: [email protected], [email protected], [email protected]
Guo Xianzhou
Affiliation:
Department of Mathematics, Hebei University of Technology, Tianjin 300130, P.R. China, e-mail: [email protected], [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 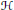$\mathcal{H}$ be a complex separable Hilbert space and 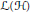$\mathcal{L}\left( \mathcal{H} \right)$ denote the collection of bounded linear operators on 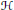$\mathcal{H}$. In this paper, we show that for any operator 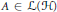$A\,\in \,\mathcal{L}\left( \mathcal{H} \right)$, there exists a stably finitely 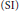$\left( \text{SI} \right)$ decomposable operator 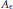${{A}_{\epsilon }}$, such that 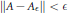$\left\| A-{{A}_{\epsilon }} \right\|\,<\,\epsilon$ and 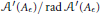${{\mathcal{A}}^{\prime }}\left( {{A}_{\epsilon }} \right)/\text{rad}\,{{\mathcal{A}}^{\prime }}\left( {{A}_{\epsilon }} \right)$ is commutative, where rad 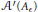${{\mathcal{A}}^{\prime }}\left( {{A}_{\epsilon }} \right)$ is the Jacobson radical of 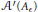${{\mathcal{A}}^{\prime }}\left( {{A}_{\epsilon }} \right)$. Moreover, we give a similarity classification of the stably finitely decomposable operators that generalizes the result on similarity classification of Cowen–Douglas operators given by C. L. Jiang.

Keywords

47A0547A5546H20K0-groupstrongly irreducible decompositionCowen–Douglas operatorscommutant algebrasimilarity classification
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 62 , Issue 2 , 01 April 2010 , pp. 305 - 319
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Aupetit, B., A Primer on Spectral Theory. Springer-Verlag, New York, 1991.Google Scholar
[2] Cao, Y., Fang, J. S. and Jiang, C. L., K-groups of Banach algebras and strongly irreducible decompositions of operators. J. Operator Theory 48(2002), no. 2, 235–253.Google Scholar
[3] Conway, J. B, Subnormal Operators. Research Notes in Mathematics 51. Pitman, Boston, MA, 1981.Google Scholar
[4] Conway, J. B, A Course in Functional Analysis. Second edition. Graduate Texts in Mathematics 96, Springer-Verlag, New York, 1990.Google Scholar
[5] Cowen, M. J. and Douglas, R. G., Complex geometry and operator theory. Acta Math. 141(1978), no. 3-4, 187–261. doi:10.1007/BF02545748Google Scholar
[6] Herrero, D. A. and Jiang, C. L., Limits of strongly irreducible operators and the Riesz decomposition theorem. Mich. Math. J. 37(1990), no. 2, 283–291. doi:10.1307/mmj/1029004135Google Scholar
[7] Jiang, C. L., Approximation of direct sum of strongly irreducible operators. Northeast. Math. J. 5(1989), no. 3, 253–254.Google Scholar
[8] Jiang, C. L., Similarity classification of Cowen-Douglas operators. Canad. J. Math. 56(2004), no. 4, 742–775.Google Scholar
[9] Jiang, C. L., Guo, X. Z., and Ji, K., K-group and similarity classifition of operators. J. Funct. Anal. 225(2005), no. 1, 167–192. doi:10.1016/j.jfa.2004.12.008Google Scholar
[10] Jiang, C. L. and Wang, Z. Y., Strongly Irreducible Operators on Hilbert Space. Pitman Research Notes in Mathematics Series 389. Longman, Harlow, 1998.Google Scholar
[11] Jiang, C. L. and Wang, Z. Y., Structure of Hilbert Space Operators. World Scientific, Hackensack, NJ, 2006.Google Scholar
[12] Jiang, Z. J. and Sun, S. L., On completely irreducible operators. Front. Math. China 1(2006), no. 4, 569–581. doi:10.1007/s11464-006-0028-4Google Scholar
[13] Putnam, C. R., The spectra of operators having resolvents of first-order growth. Trans Amer. Math. Soc. 133(1968), 505–510. doi:10.2307/1994991Google Scholar
[14] Shields, A. L., Weight shift operator and analytic function theory. In: Topics in Operator Theory. Math. Surveys 13. American Mathematical Society, Providence, RI, 1974, pp. 49–128.Google Scholar