Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-08T17:34:20.319Z Has data issue: false hasContentIssue false
  • English
  • Français

Analytic Subalgebras of Von Neumann Algebras

Published online by Cambridge University Press:  20 November 2018

Paul S. Muhly  and
Kichi-Suke Saito
Paul S. Muhly
Affiliation:
The University of Iowa,Iowa City, Iowa
Kichi-Suke Saito
Affiliation:
The University of Iowa,Iowa City, Iowa Niigata University, Niigata, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let M be a von Neumann algebra and let {αt}t∊R be a σ-weakly continuous flow on M; i.e., suppose that {αt}t∊R is a one-parameter group of *-automorphisms of M such that for each ρ in the predual, M∗, of M and for each x ∊ M, the function of t, ρ(αt(x)), is continuous on R. In recent years, considerable attention has been focused on the subspace of M, H∞(α), which is defined to be

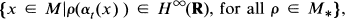
where H∞(R) is the classical Hardy space consisting of the boundary values of functions bounded analytic in the upper half-plane. In Theorem 3.15 of [8] it is proved that in fact H∞(α) is a σ-weakly closed subalgebra of M containing the identity operator such that

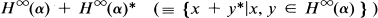
is σ-weakly dense in M, and such that

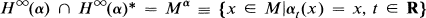
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 39 , Issue 1 , 01 February 1987 , pp. 74 - 99
Copyright
Copyright © Canadian Mathematical Society 1987

References

1. Arveson, W. B., Analyticitv in operator algebras, Amer. J. Math. 89 (1967), 578–642.Google Scholar
2. Arveson, W. B., On groups of automorphisms of operator algebras, J. Funct. Anal. 15 (1974), 217–243.Google Scholar
3. Haagerup, U., The standard form of von Neumann algebras, Math. Scand. 37 (1975), 217–243.Google Scholar
4. Haagerup, U., Operator valued weights in von Neumann algebras I, J. Funct. Anal. 32 (1979), 175–206.Google Scholar
5. Haagerup, U., Operator valued weights in von Neumann algebras II, J. Funct. Anal. 33 (1979), 339–361.Google Scholar
6. Haagerup, U., If-spaces associated with an arbitrary von Neumann algebra, Algebres d'operateurs et leurs applications en physique mathématique (Colloques internationaux du CNRS, No. 274, Marseille 20-24 Juin 1977), 175–184; (Éditions du CNRS, Paris, 1979).Google Scholar
7. Kawamurya, S. and Tomiyama, J., On subdiagonal algebras associated with flows in operator algebras, J. Math. Soc. Japan 29 (1977), 73–90.Google Scholar
8. Loebl, R. I. and Muhly, P. S., Analyticity and flows in von Neumann algebras, J. Funct. Anal. 29(1978), 214–252.Google Scholar
9. McAsey, M. J. and Muhly, P. S., Representations of non-self-adjoint crossed products., Proceedings of the London Mathematical Society, Third Series 47 (1983), 128–144.Google Scholar
10. McAsey, M., Muhly, P. S. and Saito, K.-S., Nonself adjoint crossed products (Invariant subspaces and maximality), Trans. Amer. Math. Soc. 248 (1979), 381–409.Google Scholar
11. McAsey, M., Muhly, P. S. and Saito, K.-S., Nonself adjoint crossed products II, J. Math. Soc. Japan 33 (1981), 485–495 .Google Scholar
12. McAsey, M., Muhly, P. S. and Saito, K.-S., Nonself adjoint crossed products III (Infinite algebras), J. Operator Theory 12 (1984), 3–22.Google Scholar
13. Muhly, P. S., Maximal weak*-Dirichlet algebras, Proc. Amer. Math. Soc. 36 (1972), 515–518.Google Scholar
14. Muhly, P. S., Function algebras and flows, Acta Sci. Math. (Szeged) 35 (1973), 111–121.Google Scholar
15. Saito, K.-S., On noncommutative Hardy spaces associated with flows infinite von Neumann algebras, Tôhoku Math. J. 29 (1977), 585–595.Google Scholar
16. Saito, K.-S., Invariant subspaces for finite maximal subdiagonal algebras, Pacific J. Math. 93 (1981), 431–434.Google Scholar
17. Saito, K.-S., Invariant subspaces and cocycles in nonselfadjoint crossed products, J. Funct. Anal. 45 (1982), 177–193.Google Scholar
18. Saito, K.-S., Nonself adjoint subalgebras associated with compact abelian group actions on finite von Neumann algebras, Tôhoku Math. J. 34 (1982), 485–494.Google Scholar
19. Saito, K.-S., Spectral resolutions of invariant subspaces by compact abelian group actions on von Neumann algebras, preprint.Google Scholar
20. Segal, I. E., A noncommutative extension of abstract integration, Ann. of Math. 57 (1953), 401–457.Google Scholar
21. Solel, B., Invariant subspaces for algebras of analytic operators associated with a periodic flow on a finite von Neumann algebra, preprint.CrossRefGoogle Scholar
22. Solel, B., Algebras of analytic operators associated with a periodic flow on a von Neumann algebra, preprint.Google Scholar
23. Stratila, S., Modular theory in operator algebras, (Abacus Press, Tunbridge, England, 1981).Google Scholar
24. Takesaki, M., Duality for crossed products and the structure of von Neumann algebras of type III, Acta Math. 131 (1973), 249–308.Google Scholar
25. Takesaki, M., Theory of operator algebras I, (Springer-Verlag, Berlin-Heidelberg-New York, 1979).CrossRefGoogle Scholar
26. Terp, M., Lp-spaces associated with von Neumann algebras, Rapport No. 3 (1981), The University of Odense.Google Scholar
27. Zsido, L., Spectral and ergodic properties of the analytic generators, J. Approximation Theory 20 (1977), 77–138.Google Scholar