Hostname: page-component-669899f699-vbsjw Total loading time: 0 Render date: 2025-04-27T04:54:55.604Z Has data issue: false hasContentIssue false
  • English
  • Français

Analytic Hopf Surfaces

Published online by Cambridge University Press:  20 November 2018

H. G. Helfenstein
H. G. Helfenstein*
Affiliation:
University of Ottawa
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The topological concept of H-space (7) has an analytic counterpart which so far has not been considered in the literature. We define: A complex-analytic manifold S will be called an analytic H-space if it is capable of carrying a continuous binary composition

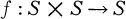
with the following properties (i) and (ii).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 14 , 1962 , pp. 329 - 333
Copyright
Copyright © Canadian Mathematical Society 1962

References

1. Caratheodory, C., Funktionentheorie, 2. Band (Basel, 1950).Google Scholar
2. Helfenstein, H., Topological H-surfaces, to appear.Google Scholar
3. Hopf, H., Ueber die Topologie der Gruppen-Mannigfaltigkeiten und ihre Verallgemeinerungen, Ann. Math., 42 (1941), 22–52.Google Scholar
4. Hu, S.-T., Homotopy theory (New York, 1959).Google Scholar
5. Huber, H., Ueber analytische Abbildungen von Ringgebieten in Ringgebiete, Compos. Math., 9 (1951), 161–168.Google Scholar
6. Nevanlinna, R., Uniformisierung (Berlin, 1953).Google Scholar
7. Serre, J.-P., Homologie singulière des espaces fibres, Ann. Math., 54, (1951), 425–505.Google Scholar