No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
Let k be an algebraically closed field and let x1, x2, . . . , xn be indeterminates. Denote by Rn the ring k[[x1, x2, … , xn]] of power series in the xi With coefficients in the field k. Let 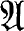 and
and 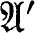 be two ideals in this ring. Then
be two ideals in this ring. Then 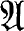 and
and 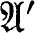 will be said to be analytically equivalent if there is an automorphism T of Rn such that T(
will be said to be analytically equivalent if there is an automorphism T of Rn such that T(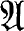 ) =
) = 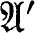 .
. 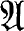 and
and 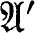 will be called analytically equivalent under T.
will be called analytically equivalent under T.
The above situation can be described geometrically as follows. The ideals 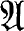 and
and 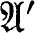 can be regarded as defining algebroid varieties V and V' in (x1, x2, … , xn)-space, and these varieties will be said to be analytically equivalent under T.
can be regarded as defining algebroid varieties V and V' in (x1, x2, … , xn)-space, and these varieties will be said to be analytically equivalent under T.
The automorphism T can be expressed by means of equations of the form :
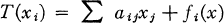
where the determinant 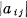 is not zero and the fi are power series of order not less than two (that is to say, containing terms of degree two or more only).
is not zero and the fi are power series of order not less than two (that is to say, containing terms of degree two or more only).