Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-18T07:05:34.893Z Has data issue: false hasContentIssue false
  • English
  • Français

Analysis of the Brylinski-Kostant Model for Spherical Minimal Representations

Published online by Cambridge University Press:  20 November 2018

Dehbia Achab  and
Jacques Faraut
Dehbia Achab
Affiliation:
Institut de Mathématiques de Jussieu, Université Pierre et Marie Curie, 4 place Jussieu, case 247, 75252 Paris email: [email protected]@math.jussieu.fr
Jacques Faraut
Affiliation:
Institut de Mathématiques de Jussieu, Université Pierre et Marie Curie, 4 place Jussieu, case 247, 75252 Paris email: [email protected]@math.jussieu.fr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We revisit with another view point the construction by R. Brylinski and B. Kostant of minimal representations of simple Lie groups. We start from a pair 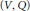$\left( V,\,Q \right)$, where 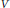$V$ is a complex vector space and 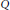$Q$ a homogeneous polynomial of degree 4 on 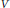$V$. The manifold $\Xi $ is an orbit of a covering of Conf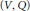$\left( V,\,Q \right)$, the conformal group of the pair 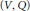$\left( V,\,Q \right)$, in a finite dimensional representation space. By a generalized Kantor-Koecher-Tits construction we obtain a complex simple Lie algebra $\mathfrak{g}$, and furthermore a real form 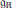${{\mathfrak{g}}_{\mathbb{R}}}$. The connected and simply connected Lie group 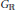${{G}_{\mathbb{R}}}$ with 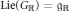$\text{Lie}\left( {{G}_{\mathbb{R}}} \right)\,=\,{{\mathfrak{g}}_{\mathbb{R}}}$ acts unitarily on a Hilbert space of holomorphic functions defined on the manifold $\Xi $.

Keywords

17C3622E4632M1533C80minimal representationKantor–Koecher–Tits constructionJordan algebraBernstein identityMeijer G-function
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 64 , Issue 4 , 01 August 2012 , pp. 721 - 754
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Achab, D., Algèbres de Jordan de rang 4 et représentations minimales. Adv. Math. 153(2000), no. 1, 155–183. http://dx.doi.org/10.1006/aima.1999.1874 Google Scholar
[2] Achab, D., Construction process for simple Lie algebras. J. Algebra 325(2011), 186–204. http://dx.doi.org/10.1016/j.jalgebra.2010.10.002 Google Scholar
[3] Allison, B. N., Models of isotropic simple Lie algebras. Comm. Algebra 7(1979), no. 17, 1835–1875. http://dx.doi.org/10.1080/00927877908822432 Google Scholar
[4] Allison, B. N., Simple structurable algebras of skew-dimension one. Comm. Algebra 18(1990), no. 4, 1245–1279. http://dx.doi.org/10.1080/00927879008823963 Google Scholar
[5] Allison, B. N. and Faulkner, J. R., A Cayley-Dickson process for a class of structurable algebras. Trans. Amer. Math. Soc. 283(1984), no. 1, 185–210. http://dx.doi.org/10.1090/S0002-9947-1984-0735416-2 Google Scholar
[6] Brylinski, R., Quantization of the 4-dimensional nilpotent orbit of SL(3; R). Canad. J. Math. 49(1997), no. 5, 916–943. http://dx.doi.org/10.4153/CJM-1997-048-0 Google Scholar
[7] Brylinski, R., Geometric quantization of real minimal nilpotent orbits. Symplectic geometry. Differential Geom. Appl. 9(1998), no. 1–2, 5–58. http://dx.doi.org/10.1016/S0926-2245(98)00017-5 Google Scholar
[8] Brylinski, R. and Kostant, B., Minimal representations, geometric quantization, and unitarity. Proc. Nat. Acad. Sci. U. S.A. 91(1994), no. 13, 6026–6029. http://dx.doi.org/10.1073/pnas.91.13.6026 Google Scholar
[9] Brylinski, R. and Kostant, B., Lagrangian models of minimal representations of E8, E7 and E8. In: Functional analysis on the eve of the 21st century, Vol. 1 (New Brunswick, NJ, 1993). Progr. Math., 131, Birkhäuser Boston, Boston, MA, pp. 13–63.Google Scholar
[10] Cartier, P., Representations of p-adic groups. a survey In: Automorphic forms, representations and L-functions, (Proc. Sympos. Pure Math., Oregon State Univ., Corvallis, Ore., 1977), Part 1, Proc. Sympos. Pure Math., 31, American Mathematical Society, Providence, RI, 1979, pp. 111–155.Google Scholar
[11] Clerc, J.-L., Special prohomogeneous vector spaces associated to F4, E6, E7, E8 and simple Jordan algebras of rank 3. J. Algebra 264(2006), no. 1, 98–128. http://dx.doi.org/10.1016/S0021-8693(03)00115-7 Google Scholar
[12] Faraut, J. and Gindikin, S., Pseudo-Hermitian symmetric spaces of tube type. In: Topics in geometry, Progr. Nonlinear Differential Equations Appl., 20, Birkhäuser Boston, Boston, MA, 1996, pp. 123–154.Google Scholar
[13] Faraut, J. and Korányi, A., Analysis on symmetric cones. Oxford Mathematical Monographs. Oxford Science Publications. The Clarendon Press, Oxford University Press, New York, 1994.Google Scholar
[14] Goodman, R., Harmonic analysis on compact symmetric spaces: the legacy of Elie Cartan and Hermann Weyl. In: Groups and analysis, London Math. Soc. Lecture Note Ser., 354, Cambridge University Press, Cambridge, 2008, pp. 1–23.Google Scholar
[15] Kobayashi, T. and Mano, G., The Schrödinger model for the minimal representation of the indefinite orthogonal group O(p; q). Mem. Amer. Math. Soc. 213(2011), no. 1000.Google Scholar
[16] Kobayashi, T. and Ørsted, B., Analysis on the minimal representation of O(p; q). I. Realization via conformal geometry. Adv. Math. 180(2003), no. 2, 486–512. http://dx.doi.org/10.1016/S0001-8708(03)00012-4Google Scholar
[17] Mathai, A. M. , A Handbook of generalized special functions for statistical and physical sciences. Oxford Science Publications. The Clarendon Press, Oxford University Press, New York, 1993.Google Scholar
[18] Paris, R. B. and Wood, A. D., Asymptotics of high order differential equations. Pitman Research Notes in Mathematics Series, 129, Longman Scientific and Technical, Harlow; John Wiley & Sons, new York, 1986.Google Scholar
[19] Pevzner, M., Analyse conforme sur les algèbres de Jordan. J. Aust. Math. Soc. 73(2002), no. 2, 279–299. http://dx.doi.org/10.1017/S1446788700008831Google Scholar
[20] Rawnsley, J. and S. Sternberg, On representations associated to the minimal nilpotent coadjoint orbit of SL(3; R). Amer. J. Math. 104(1982), no. 6, 1153–1180. http://dx.doi.org/10.2307/2374055Google Scholar
[21] Satake, I., Algebraic structures of symmetric domains. Kanoo Memorial Lectures, 4, Iwanami Shoten, Tokyo; Princeton University Press, Princeton, NJ, 1980.Google Scholar
[22] Sekiguchi, J. , Remarks on nilpotent orbits of a symmetric pair. J. Math. Soc. Japan 39(1987), no. 1, 127–138. http://dx.doi.org/10.2969/jmsj/03910127Google Scholar
[23] Torasso, P., Quantification géométrique, opérateurs d'entrelacement et representations de SL3(R). Acta Math. 150(1983), no. 3–4, 153–242. http://dx.doi.org/10.1007/BF02392971Google Scholar