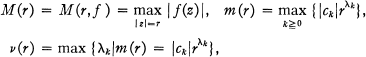Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Srivastava, G.S
and
Juneja, O.P
1981.
The maximum term of a power series.
Journal of Mathematical Analysis and Applications,
Vol. 81,
Issue. 1,
p.
1.


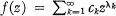 be an analytic function with radius of convergence
be an analytic function with radius of convergence