Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Prugovečki, E.
1969.
Rigorous derivation of generalized lippmann-schwinger equations from time-dependent scattering theory.
Il Nuovo Cimento B Series 10,
Vol. 63,
Issue. 2,
p.
569.


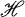 be a Hilbert space with inner product (•, •) and let
be a Hilbert space with inner product (•, •) and let 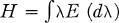 and
and 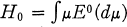 . In this paper we consider the set function
. In this paper we consider the set function 