Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-18T12:49:53.806Z Has data issue: false hasContentIssue false
  • English
  • Français

An Infinite Order Whittaker Function

Published online by Cambridge University Press:  20 November 2018

Mark McKee
Mark McKee*
Affiliation:
Department of Mathematics, University of Oklahoma, Norman, OK 73019, USA, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we construct a flat smooth section of an induced space 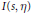$I(s,\eta )$ of 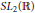$S{{L}_{2}}\left( \mathbb{R} \right)$ so that the attached Whittaker function is not of finite order. An asymptotic method of classical analysis is used.

Keywords

11F7022E4541A6011M9930D1533C15
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 2 , 01 April 2009 , pp. 373 - 381
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] de Bruijn, N. G., Asymptotic Methods in Analysis. Dover Publications, New York, 1981.Google Scholar
[2] Cogdell, J. W. and Piatetski-Shapiro, I. I., Converse theorems for GLn II. J. Reine Angew. Math. 507(1999), 165–188.Google Scholar
[3] Cohn, L., Analytic theory of the Harish–Chandra C-function. Lecture Notes in Mathematics 429, Springer-Verlag, Berlin–New York, 1974.Google Scholar
[4] Erdélyi, A., Asymptotic expansions. Dover Publications, New York, 1956.Google Scholar
[5] Gelbart, S. and Shahidi, F., Boundedness of a Automorphic L-functions in vertical strips. J. Amer. Math. Soc. 14(2001), no. 1, 79–107.Google Scholar
[6] Jacquet, H., Fonctions de Whittaker associeés aux groupes de Chevalley. Bull. Soc. Math. France 95(1967), 243–309.Google Scholar
[7] Kim, H. H., Functoriality for the exterior square of GL 4 and the symmetric fourth of GL 2, J. Amer. Math. Soc. 16(2003), no. 1, 139–183.Google Scholar
[8] Kim, H. H. and Shahidi, F., Functorial products for GL 2 × GL 3 and the symmetric cube for GL 2. Ann. of Math. 155(2002), no. 3, 837–893.Google Scholar
[9] Langlands, R., Euler products. Yale Mathematical Monographs 1, Yale University Press, New Haven, CT, 1971.Google Scholar
[10] Langlands, R., On the functional equations satisfied by Eisenstein series. Lecture Notes in Mathematics 544, Springer-Verlag, Berlin-New York, 1976.Google Scholar
[11] Mc Kee, M., On the finite order of Whittaker functions, Eisenstein series, and automorphic L-functions. Ph. D. thesis, Princeton University, 2003.Google Scholar
[12] Murray, J. D., Asymptotic analysis. Clarendon Press, Oxford, 1974.Google Scholar
[13] Schiffman, G., Intégrales d';interlacement et fonctions de Whittaker. Bull. Soc. Math. France 99(1971), 3–72.Google Scholar
[14] Shahidi, F., Functional equation satisfied by certain L-functions. Compositio Math. 37(1978), no. 2, 171–207.Google Scholar
[15] Shahidi, F.,Whittaker models for real groups. Duke Math. J. 47(1980), no. 1, 99–125.Google Scholar
[16] Shahidi, F., On certain L-functions. Amer. J. Math. 103(1981), no. 2, 297–355.Google Scholar
[17] Shahidi, F., Local coefficients as Artin factors for real groups. Duke Math. J. 52(1985), no. 4, 973–1007.Google Scholar
[18] Shahidi, F., On the Ramanujan conjecture and finiteness of poles for certain L-functions. Ann. of Math. 127(1988), no. 3, 547–584.Google Scholar
[19] Shahidi, F., A proof of Langlands’ conjecture on Plancherel measures; Complementary series for p-adic groups. Ann. of Math 132(1990), no. 2, 273–330.Google Scholar
[20] Shalika, J. A., The multiplicity one theorem for GLn. Ann. of Math. 100(1974), 171–193.Google Scholar
[21] Wallach, N. R., Real reductive groups I. Pure and Applied Mathematics 132, Academic Press, Boston, MA, 1988.Google Scholar
[22] Wallach, N. R., Real reductive groups II. Pure and Applied Mathematics 132-II, Academic Press, Boston, MA, 1992.Google Scholar