Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
1981.
Von Neumann Algebras.
Vol. 27,
Issue. ,
p.
387.
Petz, D.
1983.
On spectral and central states on Banach algebras.
Acta Mathematica Hungarica,
Vol. 42,
Issue. 1-2,
p.
19.
Petz, Dénes
and
Zemánek, Jaroslav
1988.
Characterizations of the trace.
Linear Algebra and its Applications,
Vol. 111,
Issue. ,
p.
43.
Столяров, А И
Stolyarov, A I
Тихонов, Олег Евгеньевич
Tikhonov, Oleg Evgen'evich
Шерстнев, Анатолий Николаевич
and
Sherstnev, Anatolii Nikolaevich
2002.
Характеризация нормальных следов на алгебрах фон Неймана неравенствами для модуля.
Математические заметки,
Vol. 72,
Issue. 3,
p.
448.
Tikhonov, O. E.
2005.
Subadditivity Inequalities in von Neumann Algebras and Characterization of Tracial Functionals.
Positivity,
Vol. 9,
Issue. 2,
p.
259.
Bikchentaev, Airat M.
and
Tikhonov, Oleg E.
2007.
Characterization of the trace by monotonicity inequalities.
Linear Algebra and its Applications,
Vol. 422,
Issue. 1,
p.
274.
Динь, Чунг Хоа
Dinh, Trung Hoa
Тихонов, Олег Евгеньевич
and
Tikhonov, Oleg Evgen'evich
2010.
Взвешенные неравенства монотонности для следов на операторных алгебрах.
Математические заметки,
Vol. 88,
Issue. 2,
p.
193.
Bikchentaev, A.M.
2010.
Commutativity of projections and characterization of traces on Von Neumann algebras.
Siberian Mathematical Journal,
Vol. 51,
Issue. 6,
p.
971.
Hoa, Dinh Trung
and
Tikhonov, O. E.
2010.
Weighted monotonicity inequalities for traces on operator algebras.
Mathematical Notes,
Vol. 88,
Issue. 1-2,
p.
177.
Bikchentaev, A. M.
2011.
Commutation of projections and trace characterization on von Neumann algebras. II.
Mathematical Notes,
Vol. 89,
Issue. 3-4,
p.
461.
Бикчентаев, Айрат Мидхатович
and
Bikchentaev, Airat Midkhatovich
2011.
Перестановочность проекторов и характеризация следа на алгебрах фон Неймана. II.
Математические заметки,
Vol. 89,
Issue. 4,
p.
483.
Bikchentaev, Airat M.
2011.
The Peierls-Bogoliubov inequality in C*-algebras and characterization of tracial functionals.
Lobachevskii Journal of Mathematics,
Vol. 32,
Issue. 3,
p.
175.
Hoa, Dinh Trung
2012.
On weighted monotonicity inequalities and characterizations of the traces.
Lobachevskii Journal of Mathematics,
Vol. 33,
Issue. 2,
p.
152.
Hoa, Dinh Trung
Osaka, Hiroyuki
and
Toan, Ho Minh
2013.
On generalized Powers–Størmer’s inequality.
Linear Algebra and its Applications,
Vol. 438,
Issue. 1,
p.
242.
Bikchentaev, A. M.
2015.
Commutation of Projections and Characterization of Traces on von Neumann Algebras. III.
International Journal of Theoretical Physics,
Vol. 54,
Issue. 12,
p.
4482.
Novikov, An. An.
and
Tikhonov, O. E.
2015.
Characterization of central elements of operator algebras by inequalities.
Lobachevskii Journal of Mathematics,
Vol. 36,
Issue. 2,
p.
208.
Farenick, Douglas
Kozdron, Michael J.
and
Plosker, Sarah
2016.
Spectra and variance of quantum random variables.
Journal of Mathematical Analysis and Applications,
Vol. 434,
Issue. 2,
p.
1106.
Bikchentaev, Airat Midkhatovich
2016.
Неравенство для следа на унитальной $C^*$-алгебре.
Математические заметки,
Vol. 99,
Issue. 4,
p.
483.
Bikchentaev, A. M.
2016.
Inequality for a trace on a unital C*-algebra.
Mathematical Notes,
Vol. 99,
Issue. 3-4,
p.
487.
Bikchentaev, A. M.
2019.
Metrics on Projections of the Von Neumann Algebra Associated with Tracial Functionals.
Siberian Mathematical Journal,
Vol. 60,
Issue. 6,
p.
952.
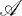 satisfies
satisfies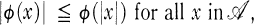
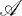
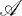 ;
;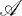 ;
;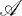 and all unitary u in Ae, the C*-lgebra formed from
and all unitary u in Ae, the C*-lgebra formed from 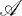 by adjunction of a unit element.
by adjunction of a unit element.