Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-24T03:24:06.508Z Has data issue: false hasContentIssue false
  • English
  • Français

An Explicit Computation of the Blanchfield Pairing for Arbitrary Links

Published online by Cambridge University Press:  20 November 2018

Anthony Conway
Anthony Conway*
Affiliation:
Université de Genève, Section de mathématiques, 2-4 rue du Lièvre, 1211 Genève, Switzerland, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a link $L$, the Blanchfield pairing 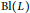$\text{Bl(}L\text{)}$ is a pairing that is defined on the torsion submodule of the Alexander module of $L$. In some particular cases, namely if $L$ is a boundary link or if the Alexander module of $L$ is torsion, 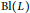$\text{Bl(}L\text{)}$ can be computed explicitly; however no formula is known in general. In this article, we compute the Blanchfield pairing of any link, generalizing the aforementioned results. As a corollary, we obtain a new proof that the Blanchfield pairing is Hermitian. Finally, we also obtain short proofs of several properties of 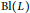$\text{Bl(}L\text{)}$.

Keywords

57M25linkBlanchfield pairingC-complexAlexander module
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 70 , Issue 5 , 01 October 2018 , pp. 983 - 1007
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Barge, Jean, Lannes, Jean, Latour, François, and Vogel, Pierre, Λ-sphères. Ann. Sci. École Norm. Sup. 7 (1975), 463–505. http://dx.doi.org/10.24033/asens.1276Google Scholar
[2] Blanchfield, Richard C., Intersection theory of manifolds with operators with applications to knot theory. Ann. of Math. 65 (1957), 340–356. http://dx.doi.Org/10.2307/1969966Google Scholar
[3] Borodzik, Maciej and Friedl, Stefan, On the algebraic unknotting number. Trans. London Math. Soc. 1 (2014), 57–84 http://dx.doi.Org/10.1112/tlms/tlu004Google Scholar
[4] Borodzik, Maciej and Friedl, Stefan, The unknotting number and classical invariants, II. Glasg. Math. J. (2014), 657-680. http://dx.doi.org/10.2140/agt.2015.15.85Google Scholar
[5] Borodzik, Maciej and Friedl, Stefan, The unknotting number and classical invariants, I. Algebr. Geom. Topol. 15 (2015), 85–135, 2015.Google Scholar
[6] Borodzik, Maciej, Stefan Friedl, and Mark Powell, Blanchfield forms and Gordian distance. J. Math. Soc. Japan 68 (2016), 1047–1080. http://dx.doi.Org/10.2969/jmsj706831047Google Scholar
[7] Choon Cha, Jae, Topological minimal genus and L2-signatures. Algebr. Geom. Topol. 8 (2008), 885–909. http://dx.doi.Org/10.2140/agt.2008.8.885Google Scholar
[8] Choon Cha, Jae, Symmetric Whitney tower cobordism for bordered 3-manifolds and links. Trans. Amer. Math. Soc. 366 (2014), 3241–3273. http://dx.doi.org/10.1090/S0002-9947-2014-06025-XGoogle Scholar
[9] Cimasoni, David, A geometric construction of the Conway potential function. Comment. Math. Helv. 79 (2004), 124–146. http://dx.doi.org/10.1007/s00014-003-0777-6Google Scholar
[10] Cimasoni, David and Florens, Vincent, Generalized Seifert surfaces and signatures of colored links. Trans. Amer. Math. Soc. 360 (2008), 1223–1264 (electronic). http://dx.doi.org/10.1090/S0002-9947-07-04176-1Google Scholar
[11] Cochran, Tim, Harvey, Shelly, and Leidy, Constance, Link concordance and generalized doubling operators. Algebr. Geom. Topol. 8 (2008), 1593–1646. http://dx.doi.Org/10.2140/agt.2008.8.1593Google Scholar
[12] Cochran, Tim, Harvey, Shelly, and Leidy, Constance, Knot concordance and higher-order Blanchfield duality. Geom. Topol. 13 (2009), 1419–1482. http://dx.doi.Org/10.2140/gt.2009.13.1419Google Scholar
[13] Cochran, Tim D. and Orr, Kent E., Not all links are concordant to boundary links. Ann. of Math. 138 (1993): 519-554. http://dx.doi.org/10.2307/2946555Google Scholar
[14] Cochran, Tim D. and Orr, Kent E., Homology boundary links and Blanchfield forms: concordance classification and new tangle-theoretic constructions. Topology 33 (1994), 397–427. http://dx.doi.org/!0.1016/0040-9383(94)90020-5Google Scholar
[15] Cochran, Tim D., Orr, Kent E., and Teichner, Peter, Knot concordance, Whitney towers and I?-signatures. Ann. of Math. (2) 157 (2003), 433–519. http://dx.doi.Org/10.4007/annals.2003.157.433Google Scholar
[16] Conway, Anthony, Friedl, Stefan, and Toffoli, Enrico, The Blanchfield pairing of colored links. Indiana Univ. Math. J. (to appear), 2017. arxiv:1609.08057v1Google Scholar
[17] Cooper, Daryl, The universal abelian cover of a link. In: Low-dimensional topology. London Math. Soc. Lecture Note Ser., 48. Cambridge University Press, Cambridge, 1982, pp. 51–66.Google Scholar
[18] Crowell, Richard H. and Strauss, Dona, On the elementary ideals of link modules. Trans. Amer. Math. Soc. 142 (1969), 93–109. http://dx.doi.org/10.1090/S0002-9947-1969-0247625-1Google Scholar
[19] Duval, Julien, Forme de Blanchfield et cobordisme d'entrelacs bords. Comment. Math. Helv. 61 (1986), 617–635. http://dx.doi.org/10.1007/BF02621935Google Scholar
[20] Friedl, Stefan, Constance Leidy, Matthias Nagel, and Mark Powell, Twisted Blanchfield pairings and decompositions of 3-manifolds. Homology, homotopy and applications, (to appear), 2017.Google Scholar
[21] Friedl, Stefan and Mark Powell, A calculation of Blanchfield pairings of 3-manifolds and knots. Moscow Math. J. 17 (2017), 59–77.Google Scholar
[22] Friedl, Stefan and Peter Teichner, New topologically slice knots. Geom. Topol. 9 (2005), 2129–2158. http://dx.doi.Org/10.2140/gt.2005.9.2129Google Scholar
[23] Hillman, Jonathan, Algebraic invariants of links. Second edition. Series on Knots and Everything, 52. World Scientific Publishing, Hackensack, NJ, 2012.Google Scholar
[24] Hillman, Jonathan, Alexander ideals of links. Lecture Notes in Mathematics, 895. Springer-Verlag, Berlin, 1981.Google Scholar
[25] Kearton, Cherry, Classification of simple knots by Blanchfield duality. Bull. Amer. Math. Soc. 79 (1973), 952–955. http://dx.doi.org/10.1090/S0002-9904-1973-13274-4Google Scholar
[26] Kearton, Cherry, Blanchfield duality and simple knots. Trans. Amer. Math. Soc. 202 (1975), 141–160. http://dx.doi.org/10.1090/S0002-9947-1975-0358796-3Google Scholar
[27] Kearton, Cherry, Cobordism of knots and Blanchfield duality. J. London Math. Soc. 10 (1975), 406–408. http://dx.doi.Org/10.1112/jlms/s2-10.4.406Google Scholar
[28] Hoon Kim, Min. Whitney towers, gropes and Casson-Gordon style invariants of links. Algebr. Geom. Topol. 15 (2015), 1813–1845. http://dx.doi.org/10.2140/agt.2015.15.1813Google Scholar
[29] Hyoung Ko, Ki, Seifert matrices and boundary link cobordisms. Trans. Amer. Math. Soc. 299 (1987), 657–681. http://dx.doi.org/10.1090/S0002-9947-1987-0869227-7Google Scholar
[30] Letsche, Carl F., An obstruction to slicing knots using the eta invariant. Math. Proc. Cambridge Philos. Soc. 128 (2000), 301–319. http://dx.doi.Org/10.1017/S0305004199004016Google Scholar
[31] Levine, Jerome, Knot modules, I. Trans. Amer. Math. Soc. 229 (1977), 1–50. http://dx.doi.org/10.1090/S0002-9947-1977-0461518-0Google Scholar
[32] Litherland, Richard A., Cobordism of satellite knots. In: Four-manifold theory. Contemp. Math., 35. Amer. Math. Soc, Providence, RI, 1984, pp. 327-362.Google Scholar
[33] Moussard, Delphine, Rational Blanchfield forms, S- equivalence, and null LP-surgeries. Bull. Soc. Math. France 143 (2015), 403–430. http://dx.doi.org/10.24033/bsmf.2693Google Scholar
[34] Powell, Mark, Twisted Blanchfield pairings and symmetric chain complexes. Quarterly J. Math. 67 (2016), 715–742.Google Scholar
[35] Ranicki, Andrew, Blanchfield and Seifert algebra in high-dimensional knot theory. Mosc. Math. J. 3 (2003), 1333–1367.Google Scholar
[36] Sheiham, Desmond, Invariants of boundary link cobordism, II. The Blanchfield-Duval form. In: Non-commutative localization in algebra and topology. London Math. Soc. Lecture Note Ser., 330. Cambridge Univ. Press, Cambridge, 2006, pp. 143–219.Google Scholar
[37] Trotter, Hale F., On S-equivalence of Seifert matrices. Invent. Math. 20 (1973), 173–207. http://dx.doi.Org/10.1007/BF01394094Google Scholar
[38] Turaev, Vladimir, Introduction to combinatorial torsions. Lectures in Mathematics ETH Zurich. Birkhâuser Verlag, Basel, 2001. Notes taken by Felix Schlenk.Google Scholar