Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Grünbaum, Branko
1970.
Polytopes, graphs, and complexes.
Bulletin of the American Mathematical Society,
Vol. 76,
Issue. 6,
p.
1131.
McMullen, Peter
and
Schneider, Rolf
1983.
Convexity and Its Applications.
p.
170.
McMullen, Peter
1986.
Angle‐sum relations for polyhedral sets.
Mathematika,
Vol. 33,
Issue. 2,
p.
173.
Budach, Lothar
1989.
Lipschitz-Killing curvatures of angular partially ordered sets.
Advances in Mathematics,
Vol. 78,
Issue. 2,
p.
140.
Budach, Lothar
1989.
On the Combinatorial Foundations of Regge‐Calculus.
Annalen der Physik,
Vol. 501,
Issue. 1,
p.
1.
McMULLEN, Peter
1993.
Handbook of Convex Geometry.
p.
933.
Leydold, Josef
and
Hörmann, Wolfgang
1998.
A sweep-plane algorithm for generating random tuples in simple polytopes.
Mathematics of Computation,
Vol. 67,
Issue. 224,
p.
1617.
Bloch, Ethan D.
2004.
Critical Points and the Angle Defect.
Geometriae Dedicata,
Vol. 109,
Issue. 1,
p.
121.
Agapito, J.
2006.
Weighted Brianchon-Gram Decomposition.
Canadian Mathematical Bulletin,
Vol. 49,
Issue. 2,
p.
161.
Bloch, Ethan D.
2010.
A Characterization of the Angle Defect and the Euler Characteristic in Dimension 2.
Discrete & Computational Geometry,
Vol. 43,
Issue. 1,
p.
100.
Woodward, Chris
2011.
Moment maps and geometric invariant theory—Corrected version (October 2011).
Les cours du CIRM,
Vol. 1,
Issue. 1,
p.
121.
Beck, Matthias
and
Robins, Sinai
2015.
Computing the Continuous Discretely.
p.
183.
Beck, Matthias
and
Robins, Sinai
2015.
Computing the Continuous Discretely.
p.
213.
Beck, Matthias
and
Robins, Sinai
2015.
Computing the Continuous Discretely.
p.
133.
Beck, Matthias
and
Robins, Sinai
2015.
Computing the Continuous Discretely.
p.
227.
Beck, Matthias
and
Robins, Sinai
2015.
Computing the Continuous Discretely.
p.
241.
Beck, Matthias
and
Robins, Sinai
2015.
Computing the Continuous Discretely.
p.
59.
Beck, Matthias
and
Robins, Sinai
2015.
Computing the Continuous Discretely.
p.
27.
Beck, Matthias
and
Robins, Sinai
2015.
Computing the Continuous Discretely.
p.
113.
Beck, Matthias
and
Robins, Sinai
2015.
Computing the Continuous Discretely.
p.
101.


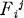 (i = 1, . . . ,ƒ
(i = 1, . . . ,ƒ