Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T06:51:33.113Z Has data issue: false hasContentIssue false
  • English
  • Français

An Application of Logic to Analysis

Published online by Cambridge University Press:  20 November 2018

Joseph Becker  and
Leonard Lipshitz
Joseph Becker
Affiliation:
Purdue University, Lafayette, Indiana
Leonard Lipshitz
Affiliation:
Purdue University, Lafayette, Indiana
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let F be a complex analytic subvariety of an open subset of Cn and p ϵ V let 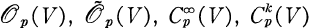be the germs at p of holomorphic, weakly holomorphic, infinitely differentiable, and k times continuously differentiate functions respectively. Spallek [15] has shown that for any p £ V there exists an integer 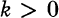such that 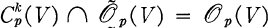, generalizing the result of Malgrange [12] that 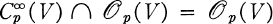.In [14], Siu proved Spallek's result from a more sheaf theoretic point of view and showed the minimal integer function 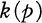is bounded on compact sets. Bloom [7] reproved Malgrange's result by using differential operators on varieties.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 28 , Issue 1 , 01 February 1976 , pp. 83 - 91
Copyright
Copyright © Canadian Mathematical Society 1976

References

1. Artin, M., Algebraic approximation of structures over complete local rings, Inst, des Hautes Etudes Scientifiques, Publ. Math. 36 (1969) 23–58.Google Scholar
2. Becker, J., Parametrizations of analytic varieties, Trans. Amer. Math. Soc. 188 (1973) 265–292.Google Scholar
3. Becker, J., Ck weakly holomorphic functions on an analytic set, Proc. Amer. Math. Soc. 39 (1973) 89–93.Google Scholar
4. Becker, J. and Polking, J., Ck weakly holomorphic functions on an analytic curve, Rice University Studies Vol. 59, No. 2, 1–12: Proceedings of the Conference on Complex Analysis.Google Scholar
5. Becker, J., Holomorphic and differentiate tangent spaces to a complex analytic variety, preprint.Google Scholar
6. Bl∞m, T., Operateurs differentials sur les espaces analytiques complexe, Séminaire Pierre Lelong, Lecture Notes in Mathematics No. 71 (Berlin-Heidelberg-New York: Springer Verlag, 1968).Google Scholar
7. Gôdel, K., Die Vollstandigkeit der Axiome des logischen Funktionenkalkuls, Monatsch Phys. 37 (1930) 349–360.Google Scholar
8. Gunning, R. C., Lectures on complex analytic varieties—local parametrization theorem (Princeton University Press, 1970).Google Scholar
9. Jacobson, N., Lectures in abstract algebra, vol. 3 (Van Nostrand 1967).Google Scholar
10. Jaffee, M., The differential operators on the curve Xa — Yb, Ph.D. Dissertation, Brandeis University, 1972.Google Scholar
11. Malgrange, B., Sur les fonctions differentiables et les ensembles analytique, Bull. Soc. Math. Frances, 91 (1963) 113–127.Google Scholar
12. Mendelson, E., Introduction to mathematical logic (Van Nostrand 1963).Google Scholar
13. Seidenberg, A., Hyperplane sections of normal varieties, Trans. Amer. Math. Soc. 69 (1950) 354–386.Google Scholar
14. Siu, Y. T., 0N approximable and holomorphic functions on complex spaces, Duke Math. J. 36 (1969) 451–454.Google Scholar
15. Spallek, K., Differzierbare und holomorphe functionen auf analytischen mengen, Math. Ann. 161 (1965) 143–163.Google Scholar
16. Stoltzenberg, G., Constructive normalization of algebraic varieties, Bull. Amer. Math. Soc. 74 (1968) 595–599.Google Scholar
17. Stutz, J., The representation problem for differential operators on analytic sets, Math. Ann. 189 (1970) 121–133.Google Scholar
18. Zariski, O. and Samuel, P., Commutative algebra vols. 1 & 2, (Toronto-London, Van Nostrand 1960).Google Scholar