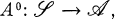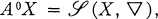Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cherenack, Paul
1983.
CONES AND COMPARISONS IN IND-AFFINE HOMOTOPY THEORY.
Quaestiones Mathematicae,
Vol. 6,
Issue. 1-3,
p.
49.
Jardine, J.F
1983.
On the homotopy groups of algebraic groups.
Journal of Algebra,
Vol. 81,
Issue. 1,
p.
180.
Jardine, J.F
1983.
Geometric models for the K-theory of fields.
Journal of Algebra,
Vol. 84,
Issue. 1,
p.
220.
Jardine, J.F
1984.
Fibrations of algebraic groups.
Journal of Algebra,
Vol. 89,
Issue. 2,
p.
335.
Cherenack, P.
1990.
Spherical unirational homotopy groups.
Journal of Pure and Applied Algebra,
Vol. 68,
Issue. 1-2,
p.
77.
Wendt, Matthias
2010.
1-Homotopy of Chevalley Groups.
Journal of K-Theory,
Vol. 5,
Issue. 2,
p.
245.
Brazelton, Thomas
2021.
Homotopy Theory and Arithmetic Geometry – Motivic and Diophantine Aspects.
Vol. 2292,
Issue. ,
p.
11.


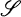 is the category of simplicial sets and
is the category of simplicial sets and 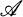 is the category of
is the category of