Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-24T17:36:10.311Z Has data issue: false hasContentIssue false
  • English
  • Français

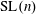$\text{SL}(n)$ Invariant Valuations on Super-Coercive Convex Functions

Part of: Polytopes and polyhedra Functions of several variables General convexity Topological linear spaces and related structures

Published online by Cambridge University Press:  25 October 2019

Fabian Mussnig
Fabian Mussnig*
Affiliation:
School of Mathematical Sciences, Tel Aviv University, 69978Tel Aviv, Israel Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

All non-negative, continuous, 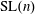$\text{SL}(n)$, and translation invariant valuations on the space of super-coercive, convex functions on 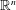$\mathbb{R}^{n}$ are classified. Furthermore, using the invariance of the function space under the Legendre transform, a classification of non-negative, continuous, 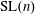$\text{SL}(n)$, and dually translation invariant valuations is obtained. In both cases, different functional analogs of the Euler characteristic, volume, and polar volume are characterized.

Keywords

valuationconvex functionsuper-coerciveLegendre transformSL(n) invariancepolar volume

MSC classification

Primary: 26B25: Convexity, generalizations
Secondary: 46A40: Ordered topological linear spaces, vector lattices 52A20: Convex sets in $n$ dimensions (including convex hypersurfaces) 52A41: Convex functions and convex programs 52B45: Dissections and valuations (Hilbert's third problem, etc.)
Type
Article
Information
Canadian Journal of Mathematics , Volume 73 , Issue 1 , February 2021 , pp. 108 - 130
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alesker, S., Continuous rotation invariant valuations on convex sets. Ann. of Math. (2) 149(1999), 997–1005. https://doi.org/10.2307/121078Google Scholar
Alesker, S., Valuations on convex functions and convex sets and Monge–Ampère operators. Adv. Geom. 19(2019), 313–322. https://doi.org/10.1515/advgeom-2018-0031CrossRefGoogle Scholar
Artstein-Avidan, S., Klartag, B., and Milman, V. D., The Santaló point of a function, and a functional form of the Santaló inequality. Mathematika 51(2004), 33–48. https://doi.org/10.1112/S0025579300015497CrossRefGoogle Scholar
Artstein-Avidan, S. and Milman, V. D., The concept of duality in convex analysis, and the characterization of the Legendre transform. Ann. of Math. (2) 169(2009), 661–674. https://doi.org/10.4007/annals.2009.169.661CrossRefGoogle Scholar
Artstein-Avidan, S. and Slomka, B. A., A note on Santaló inequality for the polarity transform and its reverse. Proc. Amer. Math. Soc. 143(2015), 1693–1704. https://doi.org/10.1090/S0002-9939-2014-12390-2CrossRefGoogle Scholar
Ball, K. M., Isometric problems in ℓ pand sections of convex sets. PhD thesis, Cambridge, 1986.Google Scholar
Barthe, F. and Fradelizi, M., The volume product of convex bodies with many hyperplane symmetries. Amer. J. Math. 135(2013), 311–347. https://doi.org/10.1353/ajm.2013.0018CrossRefGoogle Scholar
Baryshnikov, Y., Ghrist, R., and Wright, M., Hadwiger’s Theorem for definable functions. Adv. Math. 245(2013), 573–586. https://doi.org/10.1016/j.aim.2013.07.001CrossRefGoogle Scholar
Beer, G., Rockafellar, R. T., and Wets, R. J.-B., A characterization of epi-convergence in terms of convergence of level sets. Proc. Amer. Math. Soc. 116(1992), 753–761. https://doi.org/10.2307/2159443CrossRefGoogle Scholar
Blaschke, W., Über affine Geometrie VII: Neue Extremeingenschaften von Ellipse und Ellipsoid. Ber. Verh. Sächs. Akad. Wiss., Math. Phys. Kl. 69(1917), 412–420.Google Scholar
Blaschke, W., Vorlesungen über Integralgeometrie. H. 2. Teubner, Berlin, 1937.Google Scholar
Bobkov, S. G., Colesanti, A., and Fragalà, I., Quermassintegrals of quasi-concave functions and generalized Prékopa–Leindler inequalities. Manuscripta Math. 143(2014), 131–169. https://doi.org/10.1007/s00229-013-0619-9CrossRefGoogle Scholar
Bourgain, J. and Milman, V. D., New volume ratio properties for convex symmetric bodies in ℝn. Invent. Math. 88(1987), 319–340. https://doi.org/10.1007/BF01388911CrossRefGoogle Scholar
Colesanti, A. and Fragalà, I., The first variation of the total mass of log-concave functions and related inequalities. Adv. Math. 244(2013), 708–749. https://doi.org/10.1016/j.aim.2013.05.015CrossRefGoogle Scholar
Colesanti, A. and Lombardi, N., Valuations on the space of quasi-concave functions. In: Geometric aspects of functional analysis. Lecture Notes in Math., 2169, Springer, Cham, 2017, pp. 71–105.CrossRefGoogle Scholar
Colesanti, A., Lombardi, N., and Parapatits, L., Translation invariant valuations on quasi-concave functions. Studia Math. 243(2018), 79–99. https://doi.org/10.4064/sm170323-7-7CrossRefGoogle Scholar
Colesanti, A., Ludwig, M., and Mussnig, F., Minkowski valuations on convex functions. Calc. Var. Partial Differential Equations 56(2017), Art. 162. https://doi.org/10.1007/s00526-017-1243-4CrossRefGoogle ScholarPubMed
Colesanti, A., Ludwig, M., and Mussnig, F., Hessian valuations. Indiana Univ. Math. J., to appear.Google Scholar
Colesanti, A., Ludwig, M., and Mussnig, F., Valuations on convex functions. Int. Math. Res. Not. IMRN 2019 no. 8, 2384–2410. https://doi.org/10.1093/imrn/rnx189CrossRefGoogle Scholar
Dal Maso, G., An Introduction to 𝛤-Convergence. Progress in Nonlinear Differential Equations and their Applications, 8, Birkhäuser Boston, Inc., Boston, MA, 1993. https://doi.org/10.1007/978-1-4612-0327-8CrossRefGoogle Scholar
Federer, H., Geometric measure theory. Classics in Mathematics, Springer-Verlag, Berlin, Heidelberg, 1996.CrossRefGoogle Scholar
Fradelizi, M., Gordon, Y., Meyer, M., and Reisner, S., The case of equality for an inverse Santaló inequality. Adv. Geom. 10(2010), 621–630. https://doi.org/10.1515/ADVGEOM.2010.026CrossRefGoogle Scholar
Fradelizi, M. and Meyer, M., Some functional forms of Blaschke–Santaló inequality. Math. Z. 256(2007), 379–395. https://doi.org/10.1007/s00209-006-0078-zCrossRefGoogle Scholar
Fradelizi, M. and Meyer, M., Some functional inverse Santaló inequalities. Adv. Math. 218(2008), 1430–1452. https://doi.org/10.1016/j.aim.2008.03.013CrossRefGoogle Scholar
Fradelizi, M. and Meyer, M., Increasing functions and inverse Santaló inequality for unconditional functions. Positivity 12(2008), 407–420. https://doi.org/10.1007/s11117-007-2145-zCrossRefGoogle Scholar
Gruber, P. M., Convex and discrete geometry. Grundlehren der mathematischen Wissenschaften, 336, Springer-Verlag, Berlin, 2007.Google Scholar
Haberl, C. and Parapatits, L., The centro-affine Hadwiger theorem. J. Amer. Math. Soc. 27(2014), 685–705. https://doi.org/10.1090/S0894-0347-2014-00781-5CrossRefGoogle Scholar
Iriyeh, H. and Shibata, M., Symmetric Mahler’s conjecture for the volume product in the 3-dimensional case. Duke Math. J., to appear. https://doi.org/doi:10.1215/00127094-2019-0072CrossRefGoogle Scholar
Klartag, B. and Milman, V., Geometry of log-concave functions and measures. Geom. Dedicata 112(2005), 169–182. https://doi.org/10.1007/s10711-004-2462-3CrossRefGoogle Scholar
Ludwig, M., Valuations on polytopes containing the origin in their interiors. Adv. Math. 170(2002), 239–256. https://doi.org/10.1006/aima.2002.2077CrossRefGoogle Scholar
Ludwig, M., Fisher information and matrix-valued valuations. Adv. Math. 226(2011), 2700–2711. https://doi.org/10.1016/j.aim.2010.08.021CrossRefGoogle Scholar
Ludwig, M., Valuations on function spaces. Adv. Geom. 11(2011), 745–756. https://doi.org/10.1515/ADVGEOM.2011.039CrossRefGoogle Scholar
Ludwig, M., Valuations on Sobolev spaces. Amer. J. Math. 134(2012), 827–842. https://doi.org/10.1353/ajm.2012.0019Google Scholar
Ludwig, M., Covariance matrices and valuations. Adv. in Appl. Math. 51(2013), 359–366. https://doi.org/10.1016/j.aam.2012.12.003CrossRefGoogle Scholar
Ludwig, M. and Reitzner, M., A classification of SL(n) invariant valuations. Ann. of Math. (2) 172(2010), 1219–1267. https://doi.org/10.4007/annals.2010.172.1223CrossRefGoogle Scholar
Ludwig, M. and Reitzner, M., SL(n) invariant valuations on polytopes. Discrete Comput. Geom. 57(2017), 571–581. https://doi.org/10.1007/s00454-016-9838-7CrossRefGoogle Scholar
Ma, D., Real-valued valuations on Sobolev spaces. Sci. China Math. 59(2016), 921–934. https://doi.org/10.1007/s11425-015-5101-6CrossRefGoogle Scholar
Mahler, K., Ein Minimalproblem für konvexe Polygone. Mathematica (Zutphen) B7(1939), 118–127.Google Scholar
Meyer, M., Une caractérisation volumique de certains espaces normés de dimension finie. Israel J. Math. 55(1986), 317–326. https://doi.org/10.1007/BF02765029CrossRefGoogle Scholar
Milman, V. D. and Rotem, L., Mixed integrals and related inequalities. J. Funct. Anal. 264(2013), 570–604. https://doi.org/10.1016/j.jfa.2012.10.019CrossRefGoogle Scholar
Mussnig, F., Volume, polar volume and Euler characteristic for convex functions. Adv. Math. 344(2019), 340–373. https://doi.org/10.1016/j.aim.2019.01.012CrossRefGoogle Scholar
Ober, M., L p-Minkowski valuations on L q-spaces. J. Math. Anal. Appl. 414(2014), 68–87. https://doi.org/10.1016/j.jmaa.2013.12.048CrossRefGoogle Scholar
Petty, C. M., Affine isoperimetric problems. In: Discrete geometry and convexity (New York, 1982). Ann. New York Acad. Sci., 440, New York Acad. Sci., New York, 1985, pp. 113–127. https://doi.org/10.1111/j.1749-6632.1985.tb14545.xGoogle Scholar
Reisner, S., Minimal volume-product in Banach spaces with a 1-unconditional basis. J. London Math. Soc. (2) 36(1987), 126–136. https://doi.org/10.1112/jlms/s2-36.1.126CrossRefGoogle Scholar
Rockafellar, R. T., Convex analysis. Princeton Mathematical Series, 28, Princeton University Press, Princeton, NJ, 1970.CrossRefGoogle Scholar
Rockafellar, R. T. and Wets, R. J.-B., Variational analysis, Third ed., Grundlehren der mathematischen Wissenschaften, 317, Springer-Verlag, Berlin, 2009.Google Scholar
Saint-Raymond, J., Sur le volume des corps convexes symétriques. In: Initiation Seminar on Analysis: G. Choquet-M. Rogalski-J. Saint-Raymond, 20th Year: 1980/1981, Exp. No. 11, 25 pp., Publ. Math. Univ. Pierre et Marie Curie, 46, Univ. Paris VI, Paris, 1981.Google Scholar
Santaló, L. A., Un invariante afin para los cuerpos convexos del espacio des n dimensiones. Portugal. Math. 8(1949), 155–161.Google Scholar
Schneider, R., Convex Bodies: The Brunn–Minkowski theory, Second expanded ed., Encyclopedia of Mathematics and its Applications, 151, Cambridge University Press, Cambridge, 2014.Google Scholar
Tradacete, P. and Villanueva, I., Continuity and representation of valuations on star bodies. Adv. Math. 329(2018), 361–391. https://doi.org/10.1016/j.aim.2018.02.021CrossRefGoogle Scholar
Tradacete, P. and Villanueva, I., Valuations on Banach lattices. Int. Math. Res. Not. IMRN 2020 no. 1, 287–319. https://doi.org/10.1093/imrn/rny129Google Scholar
Tsang, A., Valuations on L p-spaces. Int. Math. Res. Not. IMRN 2010 no. 20, 3993–4023. https://doi.org/10.1090/S0002-9947-2012-05681-9Google Scholar
Tsang, A., Minkowski valuations on L p-spaces. Trans. Amer. Math. Soc. 364(2012), 6159–6186. https://doi.org/10.1090/s0002-9947-2012-05681-9CrossRefGoogle Scholar
Villanueva, I., Radial continuous rotation invariant valuations on star bodies. Adv. Math. 291(2016), 961–981. https://doi.org/10.1016/j.aim.2015.12.030CrossRefGoogle Scholar
Wang, T., Semi-valuations on BV(ℝn). Indiana Univ. Math. J. 63(2014), 1447–1465. https://doi.org/10.1512/iumj.2014.63.5365CrossRefGoogle Scholar