No CrossRef data available.
Published online by Cambridge University Press: 27 October 2023
We use the dual functional realization of loop algebras to study the prime irreducible objects in the Hernandez–Leclerc (HL) category for the quantum affine algebra associated with 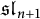 $\mathfrak {sl}_{n+1}$. When the HL category is realized as a monoidal categorification of a cluster algebra (Hernandez and Leclerc (2010, Duke Mathematical Journal 154, 265–341); Hernandez and Leclerc (2013, Symmetries, integrable systems and representations, 175–193)), these representations correspond precisely to the cluster variables and the frozen variables are minimal affinizations. For any height function, we determine the classical decomposition of these representations with respect to the Hopf subalgebra
$\mathfrak {sl}_{n+1}$. When the HL category is realized as a monoidal categorification of a cluster algebra (Hernandez and Leclerc (2010, Duke Mathematical Journal 154, 265–341); Hernandez and Leclerc (2013, Symmetries, integrable systems and representations, 175–193)), these representations correspond precisely to the cluster variables and the frozen variables are minimal affinizations. For any height function, we determine the classical decomposition of these representations with respect to the Hopf subalgebra 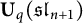 $\mathbf {U}_q(\mathfrak {sl}_{n+1})$ and describe the graded multiplicities of their graded limits in terms of lattice points of convex polytopes. Combined with Brito, Chari, and Moura (2018, Journal of the Institute of Mathematics of Jussieu 17, 75–105), we obtain the graded decomposition of stable prime Demazure modules in level two integrable highest weight representations of the corresponding affine Lie algebra.
$\mathbf {U}_q(\mathfrak {sl}_{n+1})$ and describe the graded multiplicities of their graded limits in terms of lattice points of convex polytopes. Combined with Brito, Chari, and Moura (2018, Journal of the Institute of Mathematics of Jussieu 17, 75–105), we obtain the graded decomposition of stable prime Demazure modules in level two integrable highest weight representations of the corresponding affine Lie algebra.
D.K. was partially funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) (Grant No. 446246717).