Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T06:27:05.124Z Has data issue: false hasContentIssue false
  • English
  • Français

Maximal Operator for the Higher Order Calderón Commutator

Part of: Normed linear spaces and Banach spaces; Banach lattices Harmonic analysis in several variables Integral, integro-differential, and pseudodifferential operators

Published online by Cambridge University Press:  03 September 2019

Xudong Lai
Xudong Lai*
Affiliation:
Institute for Advanced Study in Mathematics, Harbin Institute of Technology, Harbin, 150001, People’s Republic of China Email: [email protected]@mail.bnu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we investigate the weighted multilinear boundedness properties of the maximal higher order Calderón commutator for the dimensions larger than two. We establish all weighted multilinear estimates on the product of the 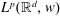$L^{p}(\mathbb{R}^{d},w)$ space, including some peculiar endpoint estimates of the higher dimensional Calderón commutator.

Keywords

MultilinearCalderón commutatormaximal operatorweighted space

MSC classification

Primary: 42B20: Singular and oscillatory integrals (Calderón-Zygmund, etc.)
Secondary: 42B25: Maximal functions, Littlewood-Paley theory 46B70: Interpolation between normed linear spaces 47G30: Pseudodifferential operators
Type
Article
Information
Canadian Journal of Mathematics , Volume 72 , Issue 5 , October 2020 , pp. 1386 - 1422
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported by National Natural Science Foundation of China (No. 11801118), China Postdoctoral Science Foundation (No. 2017M621253, No. 2018T110279), and Fundamental Research Funds for the Central Universities.

References

Bergh, J. and Löfström, J., Interpolation spaces. An introduction. Grundlehren der Mathematischen Wissenschaften, 223, Springer-Verlag, Berlin, New York, 1976.CrossRefGoogle Scholar
Calderón, A.-P., Commutators of singular integral operators. Proc. Natl Acad. Sci. USA 53(1965), 1092–1099. https://doi.org/10.1073/pnas.53.5.1092CrossRefGoogle ScholarPubMed
Calderón, A.-P., Cauchy integrals on Lipschitz curves and related operators. Proc. Natl Acad. Sci. USA 74(1977), 1324–1327. https://doi.org/10.1073/pnas.74.4.1324CrossRefGoogle ScholarPubMed
Calderón, A.-P., Commutators, singular integrals on Lipschitz curves and application. In: Proceedings of the International Congress of Mathematicians (Helsinki, 1978). Acad. Sci. Fennica, Helsinki, 1980, pp. 85–96.Google Scholar
Calderón, C. P., On commutators of singular integrals. Studia Math. 53(1975), 139–174. https://doi.org/10.4064/sm-53-2-139-174CrossRefGoogle Scholar
Coifman, R. and Meyer, Y., On commutators of singular integral and bilinear singular integrals. Trans. Amer. Math. Soc. 212(1975), 315–331. https://doi.org/10.2307/1998628CrossRefGoogle Scholar
Coifman, R. and Meyer, Y., Au delà des opérateurs pseudo-différentiels. Astérisque, 57, Société Mathématique de France, Paris, 1978.Google Scholar
Christ, M. and Journé, J. L., Polynomial growth estimates for multilinear singular integral operators. Acta Math. 159(1987), 51–80. https://doi.org/10.1007/BF02392554CrossRefGoogle Scholar
David, G. and Semmes, S., Strong A ∞ weights, Sobolev inequalities and quasiconformal mappings. In: Analysis and partial differential equations. Lecture Notes in Pure and Appl. Math., 122, Dekker, New York, 1990, pp. 101–111.Google Scholar
Ding, Y. and Lai, X., Weak type (1, 1) bound criterion for singular integral with rough kernel and its applications. Trans. Amer. Math. Soc. 371(2019), no. 3, 1649–1675. https://doi.org/10.1090/tran/7346CrossRefGoogle Scholar
Duong, X., Grafakos, L., and Yan, L., Multilinear operators with non-smooth kernels and commutators of singular integrals. Trans. Amer. Math. Soc. 362(2010), no. 4, 2089–2113. https://doi.org/10.1090/S0002-9947-09-04867-3CrossRefGoogle Scholar
Duong, X., Gong, R., Grafakos, L., Li, J., and Yan, L., Maximal operator for multilinear singular integrals with non-smooth kernels. Indiana Univ. Math. J. 58(2009), no. 6, 2517–2541. https://doi.org/10.1512/iumj.2009.58.3803CrossRefGoogle Scholar
Fefferman, C., Recent progress in classical Fourier analysis. In: Proceedings of the International Congress of Mathematicians (Vancouver, BC, 1974). Canad. Math. Congress, Montreal, Que., 1975, pp. 95–118.Google Scholar
Fong, P. W., Smoothness properties of symbols, Calderón commutators and generalizations. Thesis (Ph.D.), Cornell University, 2016.Google Scholar
García-Cuerva, J. and Rubio de Francia, J., Weighted norm inequalities and related topics. North-Holland Math. Studies, 116, North-Holland, Amsterdam, 1985.Google Scholar
Grafakos, L., Classic Fourier analysis. Third ed., Graduate Texts in Mathematics, 249, Springer, New York, 2014. https://doi.org/10.1007/978-1-4939-1194-3Google Scholar
Grafakos, L., Modern Fourier analysis. Third ed., Graduate Texts in Mathematics, 250, Springer, New York, 2014. https://doi.org/10.1007/978-1-4939-1230-8Google Scholar
Grafakos, L., Liu, L., and Yang, D., Multiple-weighted norm inequalities for maximal multi-linear singular integrals with non-smooth kernels. Proc. Roy. Soc. Edinburgh Sect. A 141(2011), no. 4, 755–775. https://doi.org/10.1017/S0308210509001383CrossRefGoogle Scholar
Hadžić, M., Seeger, A., Smart, C. K., and Street, B., Singular integrals and a problem on mixing flows. Ann. Inst. H. Poincare Anal. Non Lineaire. 35(2018), no. 4, 921–943.CrossRefGoogle Scholar
Journé, J. L., Calderón–Zygmund operators, pseudodifferential operators and the Cauchy integral of Calderón. Lecture Notes in Mathematics, 994, Springer-Verlag, Berlin, 1983. https://doi.org/10.1007/BFb0061458CrossRefGoogle Scholar
Lai, X., Multilinear estimates for Calderón commutators. Int. Math. Res. Not. IMRN. (2018). https://doi.org/10.1093/imrn/rny197CrossRefGoogle Scholar
Lerner, A. K., Ombrosi, S., Pérez, C., Torres, R. H., and Trujillo-González, R., New maximal functions and multiple weights for the multilinear Calderón–Zygmund theory. Adv. Math. 220(2009), no. 4, 1222–1264. https://doi.org/10.1016/j.aim.2008.10.014CrossRefGoogle Scholar
Léger, F., A new approach to bounds on mixing. Math. Models Methods Appl. Sci. 28(2018), no. 5, 829–849. https://doi.org/10.1142/S0218202518500215CrossRefGoogle Scholar
Meyer, Y. and Coifman, R., Wavelets. Calderón–Zygmund and multilinear operators. Cambridge Studies in Advanced Mathematics, 48, Cambridge University Press, Cambridge, 1997.Google Scholar
Seeger, A., Smart, C. K., and Street, B., Multilinear singular integral forms of Christ-Journé type. Mem. Amer. Math. Soc. 257(2019), no. 1231.Google Scholar
Stein, E. M., Singular integrals and differentiability properties of functions. Princeton Mathematical Series, 30, Princeton University Press, Princeton, NJ, 1970.Google Scholar
Stein, E. M. and Weiss, G., Interpolation of operators with change of measures. Trans. Amer. Math. Soc. 87(1958), 159–172. https://doi.org/10.2307/1993094CrossRefGoogle Scholar
Stein, E. M. and Weiss, G., Introduction to Fourier analysis on Euclidean spaces. Princeton Mathematical Series, 32, Princeton University Press, Princeton, NJ, 1971.Google Scholar