No CrossRef data available.
Article contents
Isometric dilation and Sarason’s commutant lifting theorem in several variables
Published online by Cambridge University Press: 25 February 2025
Abstract
The article deals with isometric dilation and commutant lifting for a class of n-tuples 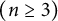 $(n\ge 3)$ of commuting contractions. We show that operator tuples in the class dilate to tuples of commuting isometries of BCL type. As a consequence of such an explicit dilation, we show that their von Neumann inequality holds on a one-dimensional variety of the closed unit polydisc. On the basis of such a dilation, we prove a commutant lifting theorem of Sarason’s type by establishing that every commutant can be lifted to the dilation space in a commuting and norm-preserving manner. This further leads us to find yet another class of n-tuples
$(n\ge 3)$ of commuting contractions. We show that operator tuples in the class dilate to tuples of commuting isometries of BCL type. As a consequence of such an explicit dilation, we show that their von Neumann inequality holds on a one-dimensional variety of the closed unit polydisc. On the basis of such a dilation, we prove a commutant lifting theorem of Sarason’s type by establishing that every commutant can be lifted to the dilation space in a commuting and norm-preserving manner. This further leads us to find yet another class of n-tuples 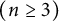 $(n\ge 3)$ of commuting contractions each of which possesses isometric dilation.
$(n\ge 3)$ of commuting contractions each of which possesses isometric dilation.
Keywords
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society



