Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-24T19:39:41.520Z Has data issue: false hasContentIssue false
  • English
  • Français

A Generalization of a Theorem of Swan with Applications to Iwasawa Theory

Part of: Algebraic number theory: global fields Algebraic number theory: local and $p$-adic fields

Published online by Cambridge University Press:  16 November 2018

Andreas Nickel
Andreas Nickel*
Affiliation:
Universität Duisburg-Essen, Fakultät für Mathematik, Thea-Leymann-Str. 9, 45127 Essen, Germany Email: [email protected]://www.uni-due.de/∼hm0251/english.html
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 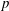$p$ be a prime and let 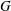$G$ be a finite group. By a celebrated theorem of Swan, two finitely generated projective 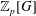$\mathbb{Z}_{p}[G]$-modules 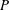$P$ and $P^{\prime }$ are isomorphic if and only if 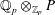$\mathbb{Q}_{p}\otimes _{\mathbb{Z}_{p}}P$ and 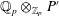$\mathbb{Q}_{p}\otimes _{\mathbb{Z}_{p}}P^{\prime }$ are isomorphic as 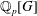$\mathbb{Q}_{p}[G]$-modules. We prove an Iwasawa-theoretic analogue of this result and apply this to the Iwasawa theory of local and global fields. We thereby determine the structure of natural Iwasawa modules up to (pseudo-)isomorphism.

Keywords

Swan’s theoremprojective latticeIwasawa algebraIwasawa theoryGalois module structure

MSC classification

Primary: 11R23: Iwasawa theory
Secondary: 11R34: Galois cohomology 11S23: Integral representations 11S25: Galois cohomology
Type
Article
Information
Canadian Journal of Mathematics , Volume 72 , Issue 3 , June 2020 , pp. 656 - 675
Copyright
© Canadian Mathematical Society 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author acknowledges financial support provided by the Deutsche Forschungsgemeinschaft (DFG) within the Heisenberg programme (No. NI 1230/3-1).

References

Ardakov, K. and Brown, K. A., Ring-theoretic properties of Iwasawa algebras: a survey. Doc. Math. (2006), Extra Vol., 7–33.Google Scholar
Ardakov, K. and Wadsley, S. J., On the Cartan map for crossed products and Hopf-Galois extensions. Algebr. Represent. Theory 13(2010), 33–41.Google Scholar
Curtis, C. W. and Reiner, I., Methods of representation theory. Vol. I. Pure and Applied Mathematics. John Wiley & Sons, New York, 1981.Google Scholar
Curtis, C. W. and Reiner, I., Methods of representation theory. Vol. II. Pure and Applied Mathematics. John Wiley & Sons, New York, 1987.Google Scholar
Hattori, A., Rank element of a projective module. Nagoya Math. J. 25(1965), 113–120.Google Scholar
Jannsen, U., Iwasawa modules up to isomorphism. In: Algebraic number theory. Adv. Stud. Pure Math., 17. Academic Press, Boston, MA, pp. 171–207.Google Scholar
McConnell, J. C. and Robson, J. C., Noncommutative Noetherian rings. Revised edition., Graduate Studies in Mathematics, 30. American Mathematical Society, Providence, RI, 2001.Google Scholar
Neukirch, J., Schmidt, A., and Wingberg, K., Cohomology of number fields. Second edition., Grundlehren der Mathematischen Wissenschaften, 323. Springer-Verlag, Berlin, 2008.Google Scholar
Nickel, A., An equivariant Iwasawa main conjecture for local fields. arxiv:1803.05743.Google Scholar
Ritter, J. and Weiss, A., Toward equivariant Iwasawa theory. Manuscripta Math. 109(2002), 131–146.Google Scholar
Serre, J.-P., Linear representations of finite groups. Graduate Texts in Mathematics, 42. Springer-Verlag, New York, 1977.Google Scholar
Swan, R. G., Induced representations and projective modules. Ann. of Math. (2) 71(1960), 552–578.Google Scholar
Swan, R. G., Algebraic K-theory. Lecture Notes in Mathematics, 76. Springer-Verlag, Berlin, 1968.Google Scholar
Witte, M., On a localisation sequence for the K-theory of skew power series rings. J. K-Theory 11(2013), 125–154.Google Scholar