No CrossRef data available.
Article contents
Combinatorics of the geometry of Wilson loop diagrams II: Grassmann necklaces, dimensions, and denominators
Published online by Cambridge University Press: 23 July 2021
Abstract
Wilson loop diagrams are an important tool in studying scattering amplitudes of SYM
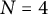 $N=4$
theory and are known by previous work to be associated to positroids. In this paper, we study the structure of the associated positroids, as well as the structure of the denominator of the integrand defined by each diagram. We give an algorithm to derive the Grassmann necklace of the associated positroid directly from the Wilson loop diagram, and a recursive proof that the dimension of these cells is thrice the number of propagators in the diagram. We also show that the ideal generated by the denominator in the integrand is the radical of the ideal generated by the product of Grassmann necklace minors.
$N=4$
theory and are known by previous work to be associated to positroids. In this paper, we study the structure of the associated positroids, as well as the structure of the denominator of the integrand defined by each diagram. We give an algorithm to derive the Grassmann necklace of the associated positroid directly from the Wilson loop diagram, and a recursive proof that the dimension of these cells is thrice the number of propagators in the diagram. We also show that the ideal generated by the denominator in the integrand is the radical of the ideal generated by the product of Grassmann necklace minors.
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2021
Footnotes
SA was partially supported by an Office of Naval Research grant. KY is supported by an NSERC Discovery grant, by the Canada Research Chair Program, and also, through some the time this work was developed, by a Humboldt Fellowship from the Alexander von Humboldt Foundation.



