Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-28T08:20:08.809Z Has data issue: false hasContentIssue false
  • English
  • Français

Cohomology of Modules Over 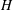$H$-categories and Co-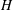$H$-categories

Part of: Abelian categories Rings and algebras arising under various constructions Hopf algebras, quantum groups and related topics

Published online by Cambridge University Press:  06 August 2019

Mamta Balodi ,
Abhishek Banerjee  and
Samarpita Ray
Mamta Balodi
Affiliation:
Department of Mathematics, Indian Institute of Science, Bangalore560012, India Email: [email protected]@[email protected]
Abhishek Banerjee
Affiliation:
Department of Mathematics, Indian Institute of Science, Bangalore560012, India Email: [email protected]@[email protected]
Samarpita Ray
Affiliation:
Department of Mathematics, Indian Institute of Science, Bangalore560012, India Email: [email protected]@[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 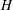$H$ be a Hopf algebra. We consider 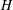$H$-equivariant modules over a Hopf module category 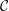${\mathcal{C}}$ as modules over the smash extension 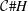${\mathcal{C}}\#H$. We construct Grothendieck spectral sequences for the cohomologies as well as the 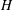$H$-locally finite cohomologies of these objects. We also introduce relative 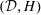$({\mathcal{D}},H)$-Hopf modules over a Hopf comodule category 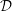${\mathcal{D}}$. These generalize relative 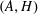$(A,H)$-Hopf modules over an 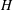$H$-comodule algebra 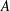$A$. We construct Grothendieck spectral sequences for their cohomologies by using their rational 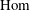$\text{Hom}$ objects and higher derived functors of coinvariants.

Keywords

H-categoryco-H-categoryH-equivariant modulerelative Hopf module

MSC classification

Primary: 16S40: Smash products of general Hopf actions
Secondary: 16T05: Hopf algebras and their applications 18E05: Preadditive, additive categories
Type
Article
Information
Canadian Journal of Mathematics , Volume 72 , Issue 5 , October 2020 , pp. 1352 - 1385
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Author M.B. was supported by SERB Fellowship PDF/2017/000229. Author A.B. was partially supported by SERB Matrics fellowship MTR/2017/000112.

References

Banerjee, A., On differential torsion theories and rings with several objects. Canad. Math. Bull. 62(2019), no. 4, 703–714. https://doi.org/10.4153/s0008439518000656CrossRefGoogle Scholar
Batista, E., Caenepeel, S., and Vercruysse, J., Hopf categories. Algebr. Represent. Theory 19(2016), 1173–1216.CrossRefGoogle Scholar
Borceux, F., Handbook of categorical algebra. 2. Categories and structures. Encyclopedia of Mathematics and its Applications, 51, Cambridge University Press, Cambridge, 1994.Google Scholar
Caenepeel, S. and Guédénon, T., On the cohomology of relative Hopf modules. Comm. Algebra 33(2005), 4011–4034. https://doi.org/10.1080/00927870500261322CrossRefGoogle Scholar
Caenepeel, S. and Fieremans, T., Descent and Galois theory for Hopf categories. J. Algebra Appl. 17(2018), no. 7, 1850120. https://doi.org/10.1142/S0219498818501207CrossRefGoogle Scholar
Cibils, C. and Solotar, A., Galois coverings, Morita equivalence and smash extensions of categories over a field. Doc. Math. 11(2006), 143–159.Google Scholar
Dăscălescu, S., Năstăsescu, C., and Raianu, Ş., Hopf algebras. An introduction. Monographs and Textbooks in Pure and Applied Mathematics, 235, Marcel Dekker, Inc., New York, 2001.Google Scholar
Estrada, S. and Virili, S., Cartesian modules over representations of small categories. Adv. Math. 310(2017), 557–609. https://doi.org/10.1016/j.aim.2017.01.030CrossRefGoogle Scholar
Grothendieck, A., Sur quelques points d’algèbre homologique. Tôhoku Math. J. (2) 9(1957), 119–221. https://doi.org/10.2748/tmj/1178244839Google Scholar
Guédénon, T., Projectivity and flatness of a module over the subring of invariants. Comm. Algebra 29(2001), 4357–4376. https://doi.org/10.1081/AGB-100106762CrossRefGoogle Scholar
Guédénon, T., On the H-finite cohomology. J. Algebra 273(2004), 455–488. https://doi.org/10.1016/j.jalgebra.2003.09.040CrossRefGoogle Scholar
Hartshorne, R., Algebraic geometry. Graduate Texts in Mathematics, 52, Springer-Verlag, New York-Heidelberg, 1977.CrossRefGoogle Scholar
Herscovich, E. and Solotar, A., Hochschild-Mitchell cohomology and Galois extensions. J. Pure Appl. Algebra 209(2007), 37–55. https://doi.org/10.1016/j.jpaa.2006.05.012CrossRefGoogle Scholar
Kashiwara, M. and Schapira, P., Categories and sheaves. Springer-Verlag, Berlin, 2006. https://doi.org/10.1007/3-540-27950-4CrossRefGoogle Scholar
Kaygun, A. and Khalkhali, M., Bivariant Hopf cyclic cohomology. Comm. Algebra 38(2010), 2513–2537. https://doi.org/10.1080/00927870903417695CrossRefGoogle Scholar
Kelly, G. M., Basic concepts of enriched category theory. London Mathematical Society Lecture Note Series, 64, Cambridge University Press, Cambridge-New York, 1982.Google Scholar
Lowen, W. and Van den Bergh, M., Hochschild cohomology of abelian categories and ringed spaces. Adv. Math. 198(2005), 172–221. https://doi.org/10.1016/j.aim.2004.11.010CrossRefGoogle Scholar
Lowen, W. and Van den Bergh, M., Deformation theory of abelian categories. Trans. Amer. Math. Soc. 358(2006), 5441–5483. https://doi.org/10.1090/S0002-9947-06-03871-2CrossRefGoogle Scholar
Lowen, W., Hochschild cohomology with support. Int. Math. Res. Not. IMRN 2015 no. 13, 4741–4812. https://doi.org/10.1093/imrn/rnu079CrossRefGoogle Scholar
Mitchell, B., Rings with several objects. Advances in Math. 8(1972), 1–161. https://doi.org/10.1016/0001-8708(72)90002-3CrossRefGoogle Scholar
Mitchell, B., Some applications of module theory to functor categories. Bull. Amer. Math. Soc. 84(1978), no. 5, 867–885. https://doi.org/10.1090/S0002-9904-1978-14530-3CrossRefGoogle Scholar
Murfet, D., Rings with several objects. http://www.therisingsea.org/notes/RingsWithSeveralObjects.pdf.Google Scholar
Schauenburg, P., Hopf algebra extensions and monoidal categories. In: New directions in Hopf algebras. Math. Sci. Res. Inst. Publ., 43, Cambridge Univ. Press, Cambridge, 2002, pp. 321–381.Google Scholar
Stănescu, A. and Ştefan, D., Cleft comodule categories. Comm. Algebra 41(2013), no. 5, 1697–1726. https://doi.org/10.1080/00927872.2011.649506CrossRefGoogle Scholar
Stenström, B., Rings of quotients. Die Grundlehren der Mathematischen Wissenschaften, 217, An introduction to methods of ring theory, Springer-Verlag, New York-Heidelberg, 1975.CrossRefGoogle Scholar
Takeuchi, M., A correspondence between Hopf ideals and sub-Hopf algebras. Manuscripta Math. 7(1972), 251–270. https://doi.org/10.1007/BF01579722CrossRefGoogle Scholar
The Stacks project, 2018. https://stacks.math.columbia.edu/tag/015Y.Google Scholar
Ulbrich, K.-H., Smash products and comodules of linear maps. Tsukuba J. Math. 14(1990), 371–378. https://doi.org/10.21099/tkbjm/1496161459CrossRefGoogle Scholar
Xu, F., On the cohomology rings of small categories. J. Pure Appl. Algebra 212(2008), no. 11, 2555–2569.CrossRefGoogle Scholar
Xu, F., Hochschild and ordinary cohomology rings of small categories. Adv. Math. 219(2008), 1872–1893. https://doi.org/10.1016/j.aim.2008.07.014CrossRefGoogle Scholar