Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T06:53:59.203Z Has data issue: false hasContentIssue false
  • English
  • Français

Abelian Surfaces with an Automorphism and Quaternionic Multiplication

Published online by Cambridge University Press:  20 November 2018

Matteo Alfonso Bonfanti  and
Bert van Geemen
Matteo Alfonso Bonfanti
Affiliation:
Dipartimento di Matematica, Università di Milano, 20133 Milano, Italia e-mail: [email protected] e-mail: [email protected]
Bert van Geemen
Affiliation:
Dipartimento di Matematica, Università di Milano, 20133 Milano, Italia e-mail: [email protected] e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We construct one-dimensional families of Abelian surfaces with quaternionic multiplication, which also have an automorphism of order three or four. Using Barth's description of the moduli space of (2,4)-polarized Abelian surfaces, we find the Shimura curve parametrizing these Abelian surfaces in a specific case. We explicitly relate these surfaces to the Jacobians of genus two curves studied by Hashimoto and Murabayashi. We also describe a (Humbert) surface in Barth's moduli space that parametrizes Abelian surfaces with real multiplication by 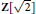$\mathbf{Z}\left[ \sqrt{2} \right]$ .

Keywords

14K1011G1014K20abelian surfacesmodulishimura curves
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 68 , Issue 1 , 01 February 2016 , pp. 24 - 43
Copyright
Copyright © Canadian Mathematical Society 2016

References

[B] Barth, W., Abelian surfaces with (1, 2)-polarization. In: Algebraic geometry, Sendai, 1985, Adv. Stud. Pure Math. 10, North-Holland, Amsterdam, 1987, pp. 41–84.Google Scholar
[BL] Birkenhake, C. and Lange, H., Complex Abelian varieties. Second ed., Grundlehren der Mathematischen Wissenschaften, 302, Springer-Berlag, Berlin, 2004.Google Scholar
[BW] Birkenhake, C. and Wilhelm, H., Humbert surfaces and the Kummer plane. Trans. Amer. Math. Soc. 335(2003), no. 5, 1819–1841. http://dx.doi.org/10.1090/S0002-9947-03-03238-0 Google Scholar
[M] Bosma, W., Cannon, J., and Playoust, C., The Magma algebra system I. The user language. Computational algebra and number theory (London, 1993). J. Symbolic Comput. 24(1997),no. 3-4, 235–265.http://dx.doi.org/10.1006/jsco.1996.0125 Google Scholar
[CQ] Cardona, G. and Quer, J., Field of moduli and field of definition for curves of genus 2. In: Computational aspects of algebraic curves, Lecture Notes Ser. Comput., 13, World Sci. Publ., Hackensack, NJ, 2005, pp. 71–83.Google Scholar
[E] Elkies, N. D., Shimura curve computations via K3 surfaces of Neron-Severi rank at least 19. In: Algorithmic number theory, Lecture Notes in Comput. Sci., 5011, Springer, Berlin, 2008, pp. 196–211.Google Scholar
[F] Freitag, E., Siegelsche Modulfunktionen. Grundlehren der Mathematischen Wissenschaften, 254, Springer-Verlag, Berlin, 1983.Google Scholar
[GS] Garbagnati, A. and Sarti, A., Kummer surfaces and K3 surfaces with (Z/2Z)4 symplectic action. arxiv:1305.3514Google Scholar
[vG] van Geemen, B., Projective models of Picard modular varieties. In: Classification of irregular varieties, Lecture Notes in Mathematics, 1515, Springer, Berlin, 1992, pp. 68–99.Google Scholar
[GP1] Gross, M. and Popescu, S., Equations of(l, d)-polarized Abelian surfaces. Math. Ann. 310(1998), no. 2, 333–377.http://dx.doi.org/10.1007/s002080050151 Google Scholar
[GP2] Gross, M. and Popescu, S., Calabi-Yau three-folds and moduli of Abelian surfaces II. Trans. Amer. Math. Soc. 363(2011), 3573–3599.http://dx.doi.org/10.1090/S0002-9947-2011-05179-2 Google Scholar
[HM] Hashimoto, K. and Murabayashi, N., Shimura curves as intersections of Humbert surfaces and defining equations of QM-curves of genus two. Tohoku Math. J. 47(1995), no. 2, 271–296.http://dx.doi.org/10.2748/tmj71178225596 Google Scholar
[HKW] Hulek, K., Kahn, C., and Weintraub, S. H., Moduli spaces of Abelian surfaces: compactification, degenerations, and Theta functions, de Gruyter Expositions in Mathematics, 12, Walter de Gruyter, Berlin, 1993.Google Scholar
[I] Igusa, J., Arithmetic variety of moduli for genus two. Ann. of Math. 72(1960), 612–649.http://dx.doi.Org/10.2307/1970233 Google Scholar
[12] Igusa, J., Theta functions. Die Grundlehren der mathematischen Wissenschaften, 194, Springer-Verlag, New York-Heidelberg, 1972.Google Scholar
[Me] Mestre, J-F., Construction de courbes de genre 2 à partir de leurs modules., In: Effective methods in algebraic geometry, Progr. Math., 94, Birkhäuser Boston, Boston, MA, 1991, pp. 313–334.Google Scholar
[PS] Petkova, M. and Shiga, H., A new interpretation of the Shimura curve with discriminant 6 in terms of Picard modular forms. Arch. Math. (Basel) 96(2011), no. 4, 335–348.Google Scholar
[R] Rotger, V., Shimura curves embedded in Igusa's threefold. In: Modular curves and Abelian varieties, Progr. Math., 224, Birkhäuser, Basel, 2004, pp. 263–276.Google Scholar